A parametric curve in a plane is a pair of functions such as
where the functions define ordered pairs (x , y). A parametric curve is a curve that is drawn in "time". In other words, the location (X, Y) of a point is based on the "time" at which the curve is being drawn. Therefore, t or range of t will determine the curve. We might say that x and y "vary" with time t.
Lets begin by first graphing some general parametric equations.
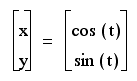

The above graph, based upon cos and sin, recall that cos and sin have a normal cycle or period of pi, therefore the range is 0 to pi. By restricting the range of t less that pi can be seen by the following examples.
1.) t = 1
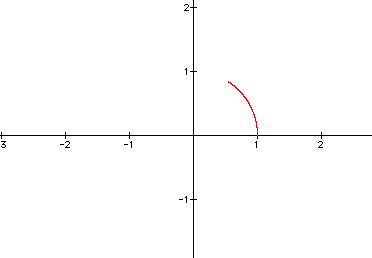
2.) t = pi/2
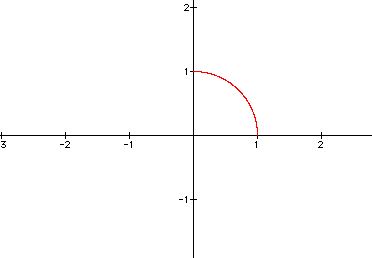
3.) t = pi
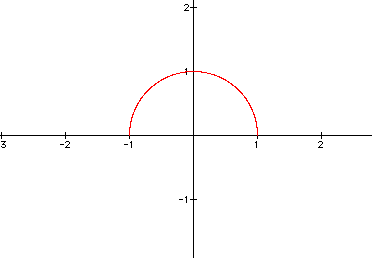
4.) t = 3pi/2
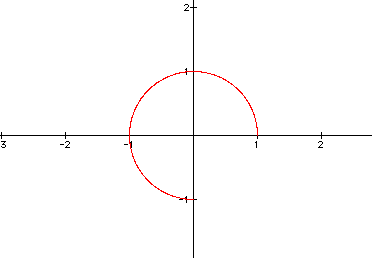
As you can see, as t ranges from 1 through 3pi/2 the arc of the curve is increasing. Or think of t being time which is increasing!
Now, let explore the following parametric equations as we vary a and b.
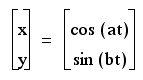
Initially, again, if we allow t to range between 0 and pi, then the following graph is generated.
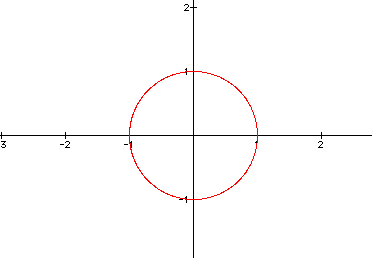
Now, lets vary a and b over the same range of t.
1.) a = 2, b = 3
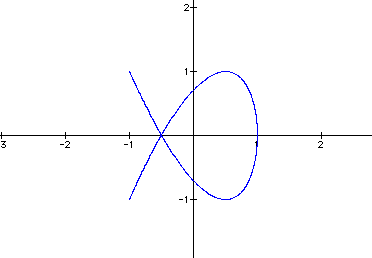
2.) a = 1/2, b = 3
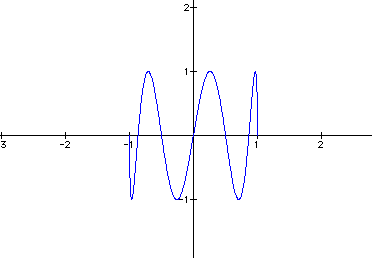
3.) a = 10, b = 3
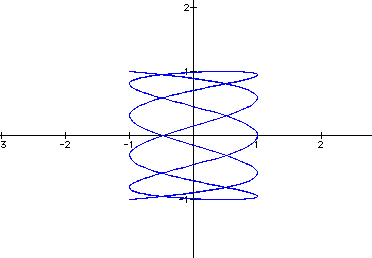
4.) a = 50, b = 3
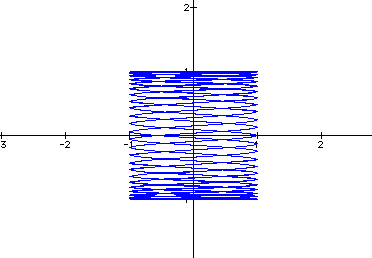
5.) a = 4, b = 20
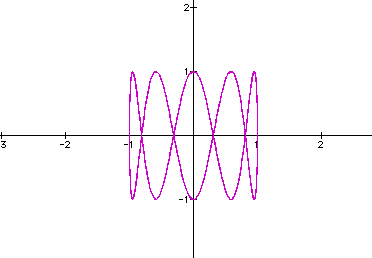
6.) a = 10, b = 100
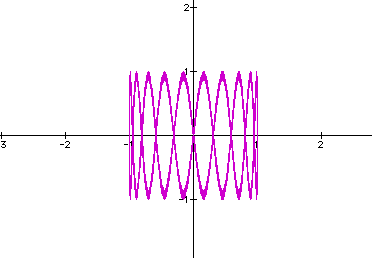
Finally, lets explore the following equations:
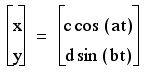
1.) a = 5, b = 8, c = 2, d = 8
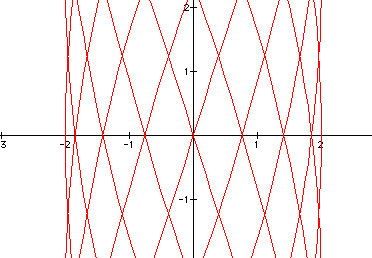
2.) a = 5, b = 9, c = 11, d = 10