The graphs generated by polar equations are
some of the most beautiful in all of mathematics. Before exploring
the graphs lets briefly define what polar equations are. Polar
equations are derived from polar coordinates, p,
of the form (r, 
), given an initial ray with endpoint as the origin
and where r is the radius and theta is the angle
the radius makes with the given ray.
Lets take a look at a basic curve.
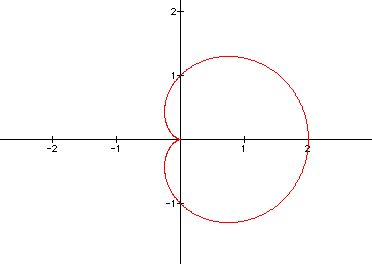
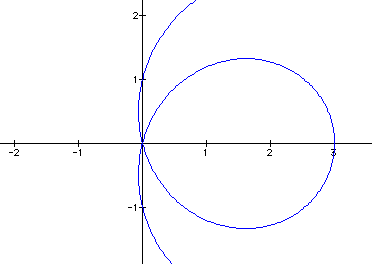
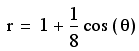
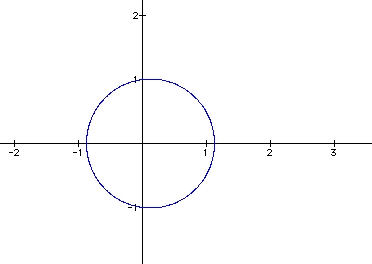
What we see as the coefficient of cos changes the "inner" circle either gets smaller or non existent or increases in size. When the inner circle increase the outer circle increase in relation.
Now lets have some fun with the beauty of these equations.
1.) 
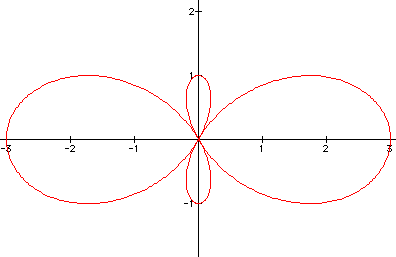
2.) 
3.) 
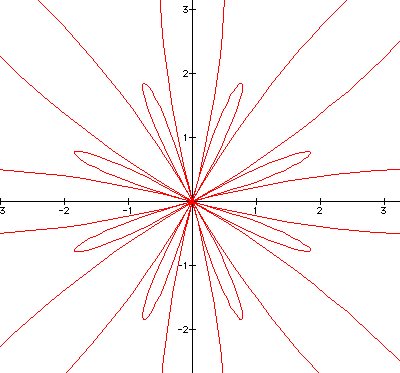
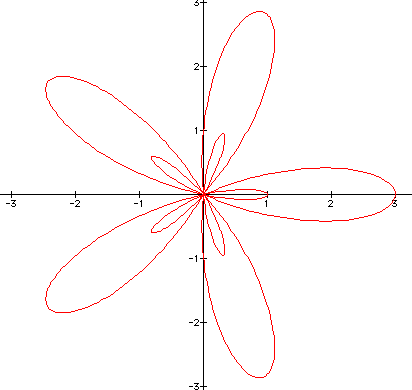
In this series of curves, called rose petals, we will explore the general equation
where we will keep a and b constant and vary k. When k = 1 there is one petal. As you see, when k = n we will have n petals! Lets start.
1.) 
(one
petal)
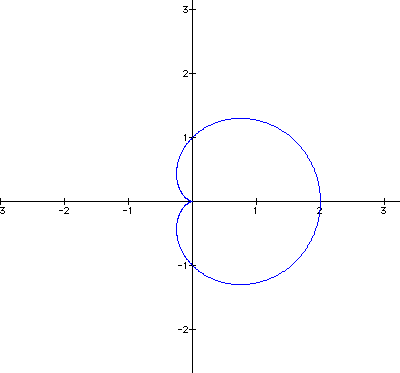
2.) 
(two
petals)
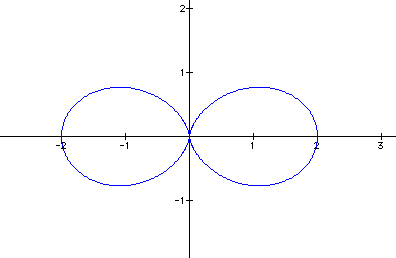
3.) 
(three
petals)
4.) 
(ten
petals)
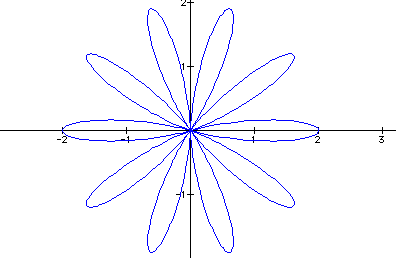
5.) 
(fifty
petals)
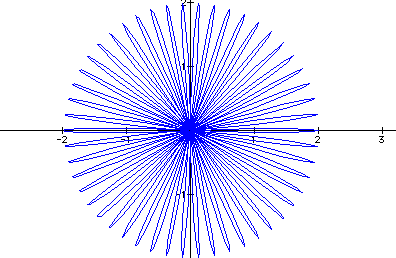
6.) 
(two
thousand petals!)
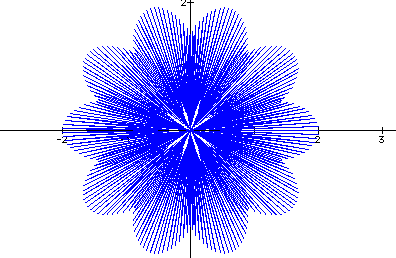
So, what can we say about the change of k? Well, we know that as k increases so do the petals. However, as the petals increase they become more difficult to see and the beauty of the curve becomes apparent.