

To begin our exploration of second degree equations, lets first consider the general equation which can be written in the form:
The graph of the equation has the following form. The graph of a second degree equation or quadratic equation is a special type of U-shaped curve called a parabola. These types of curves occur in many real life situations or applications---especially situations involving reflective properties, such as the inside of your eyes, satellite dishes, and flashlight reflectors.
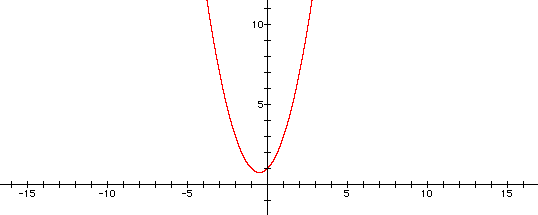
As a starting point, lets first take a look at the graph of
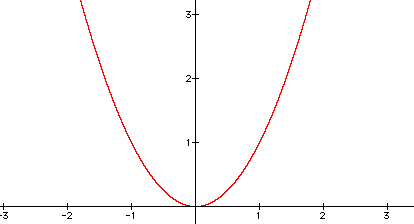
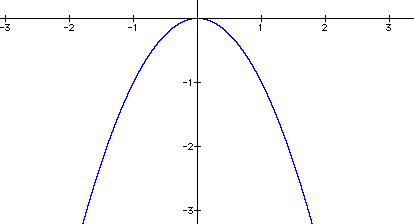
Notice that the bottom of the curve, called the vertex is centered at the origin on the Cartesian coordinate system. We can invert the graph by simply putting a minus in front of the x-squared term. Here the parabola
Now returning to our original equation lets see what happens when we "plug-in" values for a, b, and c. We will start with the integer 2 by replacing individually for a, then b, then c.
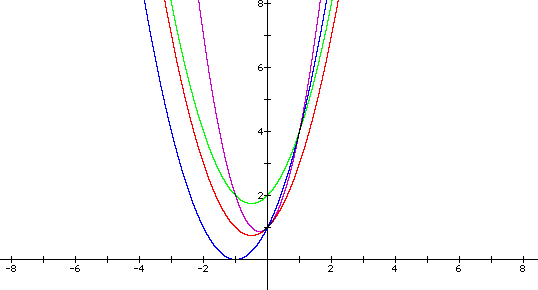
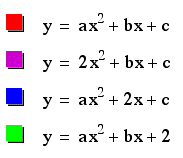
By replacing the a coefficient with 2 has the effect of narrowing the curve. By replacing the b coefficient by 2 has the effect of shifting the whole curve to the left by two units. Finally, by replacing c with 2 has the effect of shifting the whole curve up by two units.
Now, let set b=1, c=2 and let a be 2, 1/4, 0, and -2.
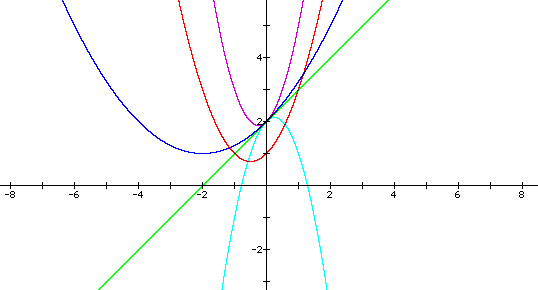
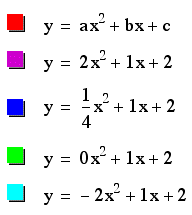
In summary, the coefficient a has the effect of either narrowing or widening the curve. The coefficient b has the effect of shifting the curve horizontally, that is, left of right. Finally, c has the effect of shifting the curve vertically or up/down.