Let's begin our exploration of the centers of a triangle. Intuitively, we might think that there is a single center to a triangle. From our understanding of other objects such as squares or circles there exists a single center of the object. However, triangles may have several centers depending on how they are constructed and define. We shall take a look at the following centers: centroid, Circumcenter, and Orthocenter.
We will begin by constructing the centroid of a triangle, such as the following.
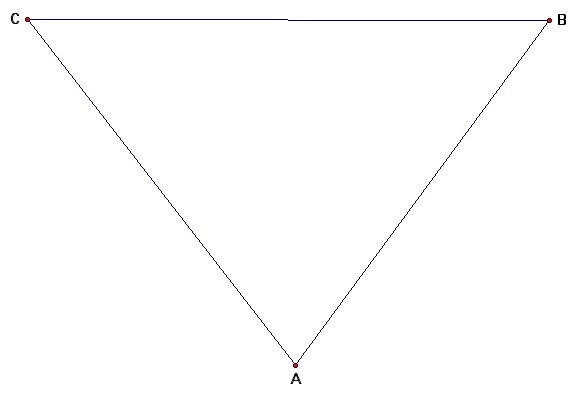
The above triangle does not need to be any special shape. Our goal is to find the centroid, we is defined as the common intersection of the three medians. A median of a triangle is the segment from a vertex to the midpoint of the opposite side. The vertices are the three end points of the triangle denoted as A, B, and C. Now we want to find the midpoint of each line segment and connect a vertex to its opposite midpoint.
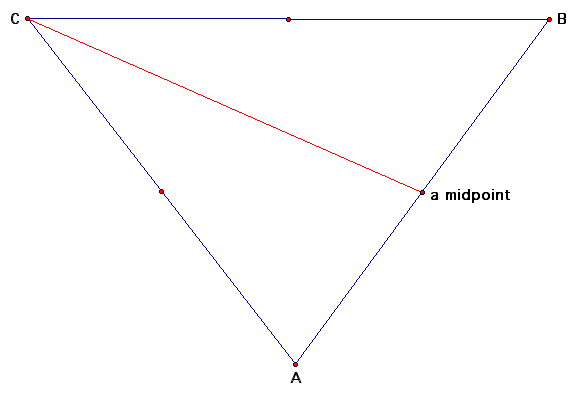
Here, a line segment was created from point C to its opposite midpoint. In the next figure, we will construct the other two line segments.
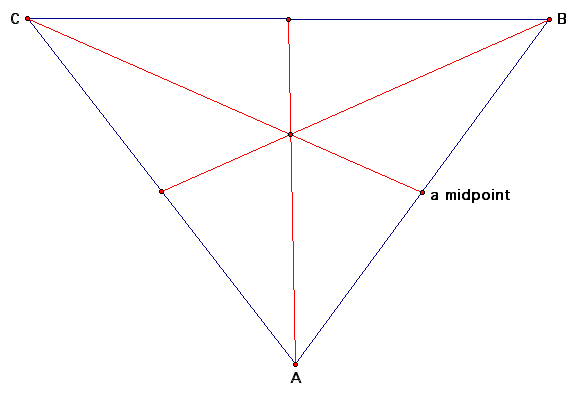
The point at the intersection of the three line segments is the centroid.
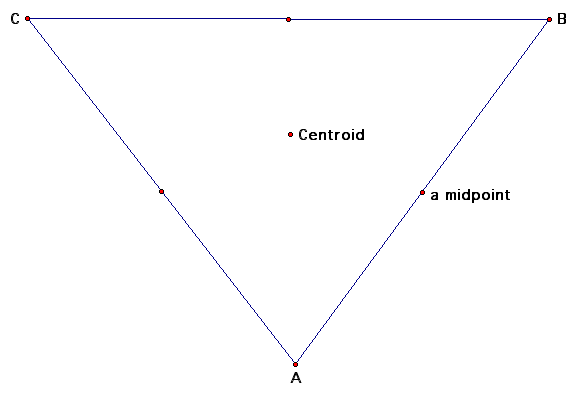
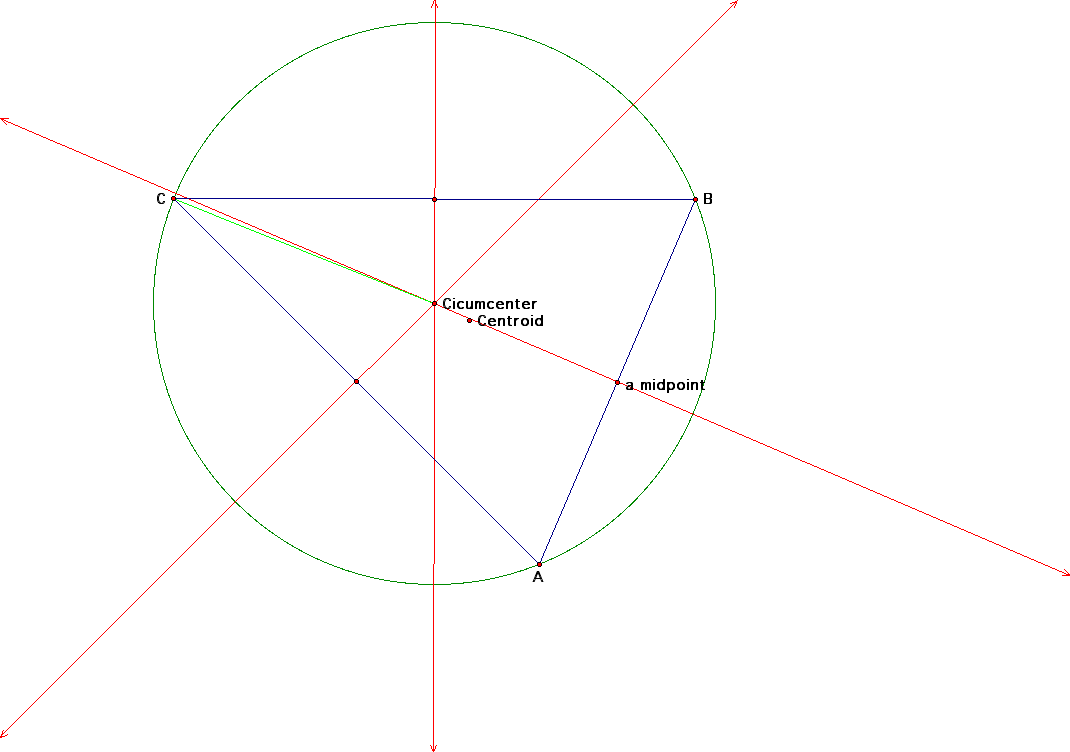
Now we turn our focus to the Circumcenter of the triangle which is defined as the point in the plane equidistant from the three vertices of the triangle. Since a point equidistant from two points lies on the perpendicular bisector of the segment determined by the two points, the Circumcenter is on the perpendicular bisector of each side of the triangle. This center may lie outside of the triangle.
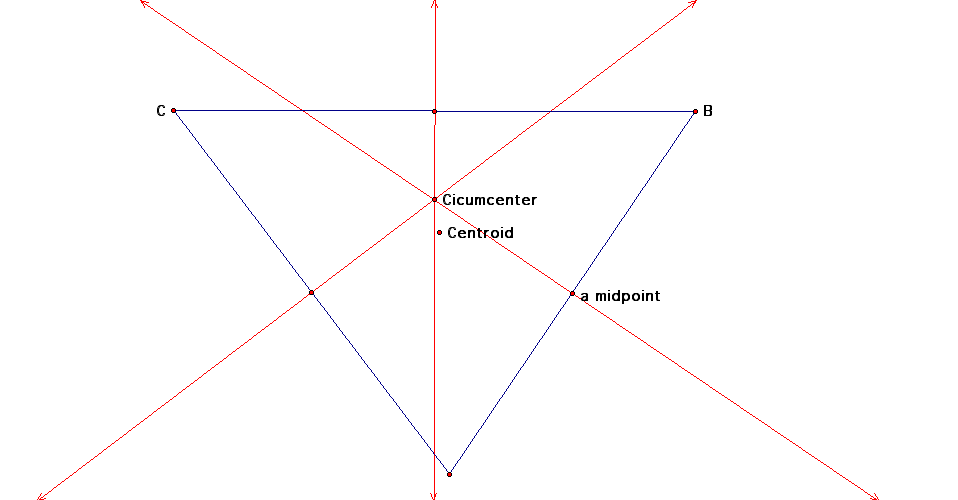
Here we have found the Circumcenter. Now lets rotate the triangle and see what effect it has on the two centers we have constructed.
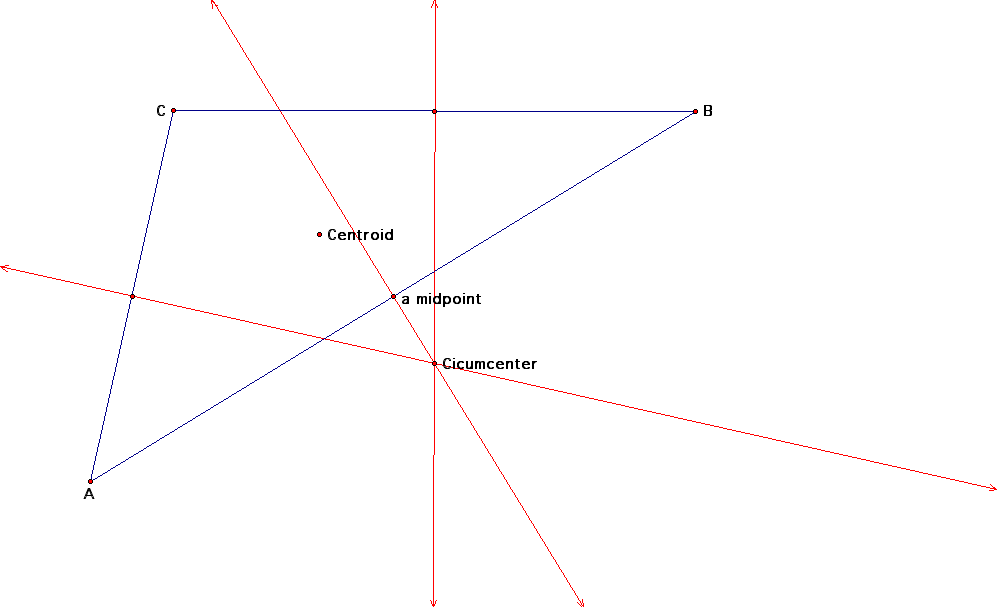
Notice that by rotating the triangle both the centroid and the Circumcenter have moved. In fact, the Circumcenter is seen "outside" the triangle.