

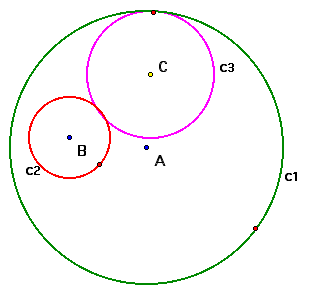
In this exercise we will explore a circle tangent to two given circles. For our investigation, we will The Geometer's Sketchpad (GPS) to make a construction. When completed our result will look like the following below.
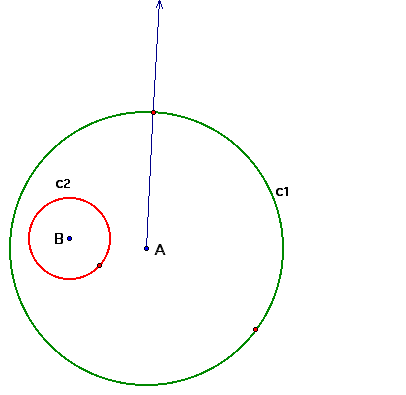
Lets begin by constructing two circles. One circle within a larger circle. The centers of each are labeled A and B. Select a point on c1 by using the "point on circle" command under the "Construct" option. This allows the point to "movable". Then construct a line from A through the selected "movable" point.
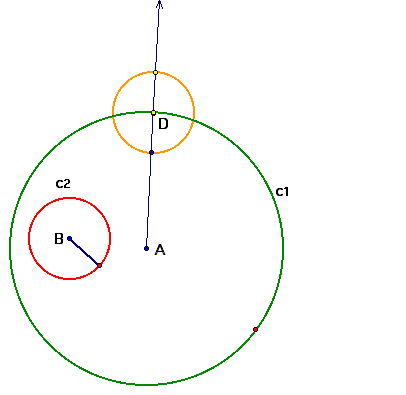
Now, construct the radius of c2 and use that radius to construct a new circle using the "Construct" command: "circle by center + point", lets call the new center D.
Create a line segment from B to E. With that line segment in place, find its mid-point M. Select both M and the segment and construct a perpendicular line. Where that line intersects AD select that point.
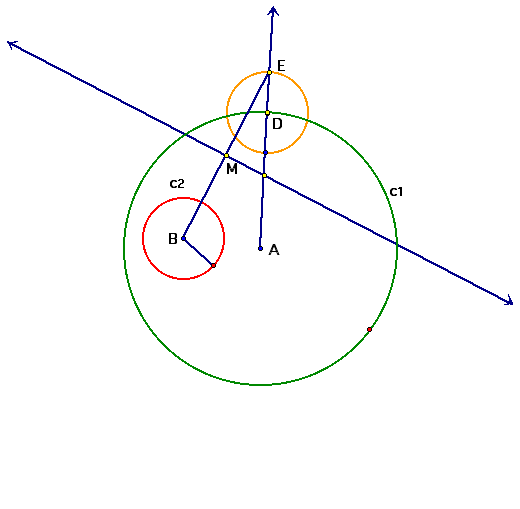
Now, construct a line segment from B to F. Using FD as the radius, construct a new circle, c4. Notice that c4 is tangent, i.e. touching, c1 and c2!
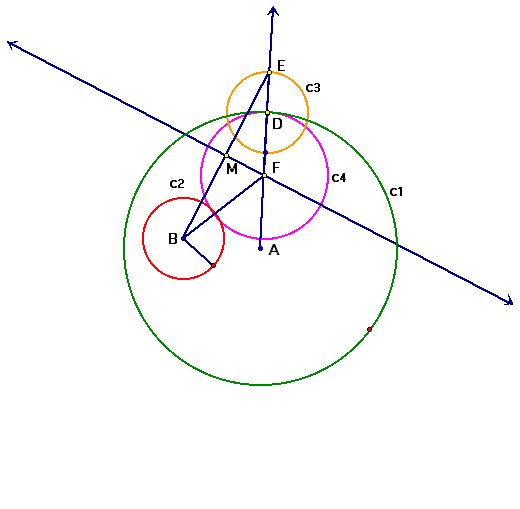
By hiding all our construction lines and points, the final result is as we showed at the top of the page.
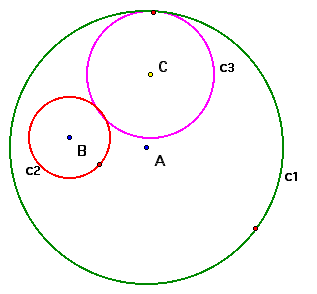
Now that we've constructed our tangent circles what can we say about the relationship of the circles? That is, what happens when we move our "movable" point on the large circle c1? Let do some examples and see what happens.
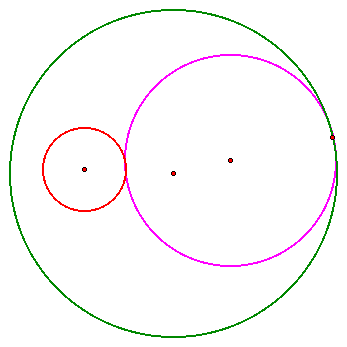
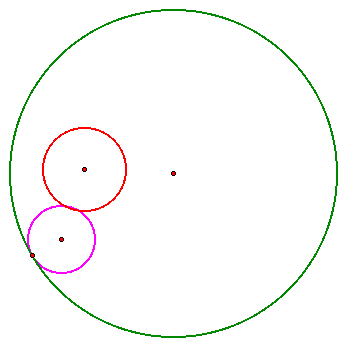
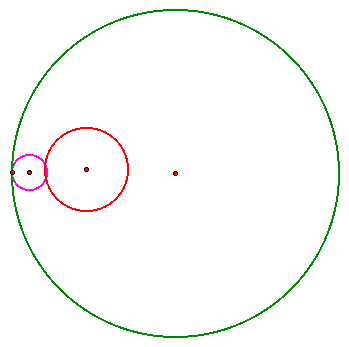
Again, what can we say about effects of moving the purple circle? Well, because of fact that it is tangent to the green and red circles, changing its position only continues its tangency.