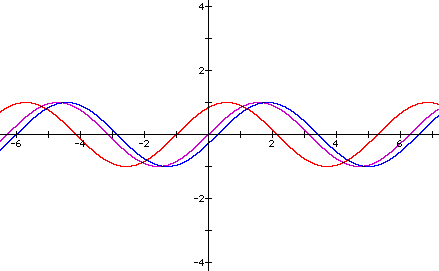
To begin, lets first consider the sin graph as shown below.
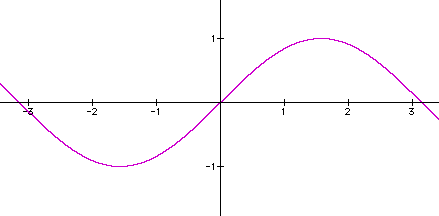
The graph of the sin function is a sine curve which appears as a wave. The graph represents one period of the function and is called one cycle of the sine curve. Although the above graph only shows a portion of the sin graph, the basic sin curve repeats indefinitely to the right and to the left. Recall that the domain of the sin function is the set of all real numbers.
Now, lets consider the the graph of the function y = a sin(bx+c).
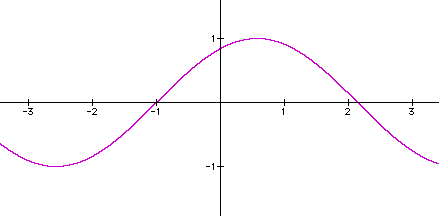
The a in the above equation refers to the amplitude. To see the effects of a notice the following graphs.
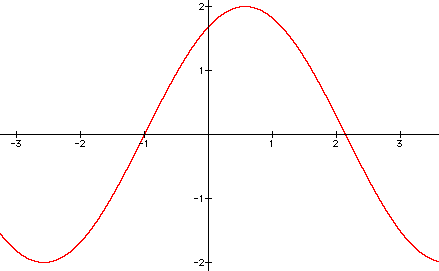
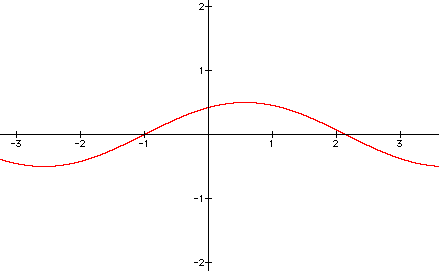
Notice that in case 1 where a = 2 the graph has a vertical stretch where the high and low parts of the graph have increased/decrease by a factor of 2. Conversely, case 2 shrinks the graph by a factor of 1/2.
Now lets take a look horizontal stretching of the graph of y = a sin(bx +c), that is, the effect of bx.
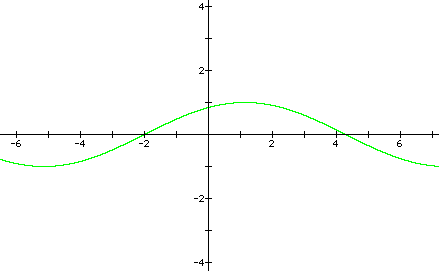
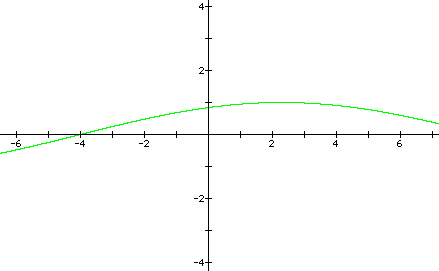
In both of the above examples, the effect of changing bx is to stretch the sin curve horizontally.
Finally, lets consider what occurs when c is changed in y = a sin(bx + c).

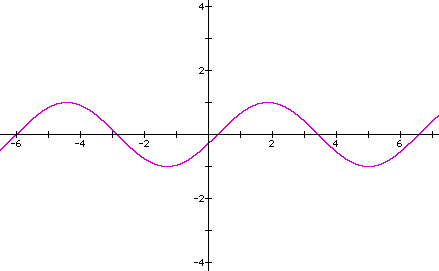
As the two graphs show, the sin curve shifts horizontally to the left. As a comparison, lets show the basic curve and shifted graphs.