Part A
We will begin our investigation by considering any triangle ABC and a point P inside the ABC. We will construct line AP, BP, and CP and extend those lines to their intersections with the opposite sides in points D, E, and F respectively. Once constructed we will explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P.
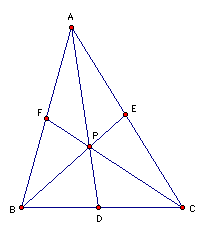
Now lets explore the product of line segments AF, BD, & EC and FC, DC, & EA.
1.) (AF)(BD)(EC):
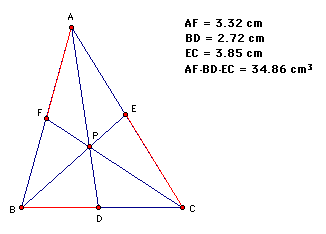
2.)(FB)(DC)(EA):
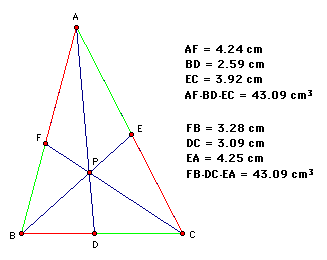
Initially the first observation we can make is that the products are equal as long as the points remain relatively unchanged in relationship to one another and that P stays inside the triangle.
Now let consider the ratios of the products (AF/FB) * (BD/DC) * (EC/EA):
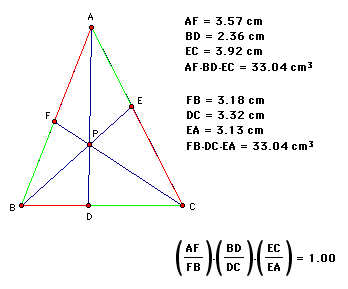
No matter how we alter the triangle the product of the ratios will always be 1. Why?
Part B: The Proof
From part A we saw that the product of ratios equal 1. Will this always be the case?
Prove that
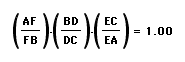
Consider the above construction we started with. The overall strategy will be to pass through point P with a line which is parallel to each of the three sides of ABC in separate constructions. Doing this will allow us to locate similar triangles in each construction. Having found the similar triangles we can relate their sides and find equalities. In the end we will bring all equalities together as a product which we will show is 1. By constructing a line through P and parallel to AB we can determine congruent angles which leads to similar triangles.
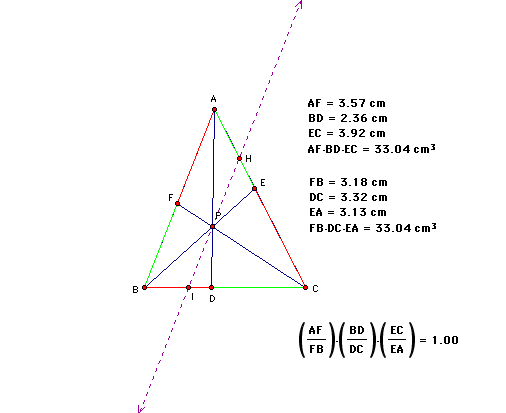
Notice that the angle AFC is congruent to HPC as well as FAC is congruent to PHC. This means that triangles AFC and HPC are similar or AF/HP = FC/PC.
Now notice that the triangles BFC and IPC are similar or BF/IP = FC/PC. By the above we could also write AF/BF = HP/IP.
We also can see that triangles BAE and HPE are similar, then HP/AB = PE/BE.
Continuing, we see that triangle BAD is similar to IPD, then IP/BA = PD/AD.
So, AF/BF = HP/IP = (HP/AB)/(IP/AB) = (PE/BD)/(PD/AD).
Now lets construct another parallel line through P parallel to BC.

As we did in the above section, we will locate similar triangles.
ABD is similar to AJP and PAK is similar to DAC resulting in BD/JP = AD/AP and DC/PK = AD/AP. This, then, implies BD/DC = JP/PK
and PE/BE = PK/BC giving us FP/FC = JP/BC.
Therefore, BD/DC = PJ/PK = (PJ/BC)/(PK/BC) = (FP/FC)/(PE/BE).
Finally, rounding out our constructions, lets consider a line through P parallel to AC.
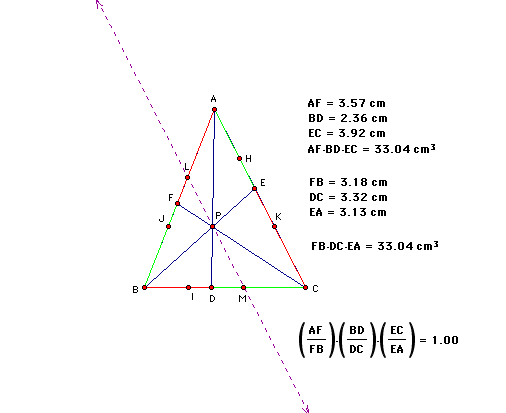
Again, following the above process, we will locate similar triangles and relate to one-another.
BEC is similar to BPM, EC/PM = BE/BP.
ABE is similar to LBP, AE/LP = BE/BP which implies that EC/PM = AE/LP
CDA is similar to DPM, PM/AC = PD/AD
AFC is similar to FLP, LP/AC = FP/FC
So, EC/AE = PM/LP =(PM/AC)/(LP/AC)= (PD/AD)/(FP/FC).
Now let put it all together.
(AF/FB) * (BD/DC) * (EC/EA) = (PE/BD)/(PD/AD) * (FP/FC)/(PE/BE) * (PD/AD)/(FP/FC) = 1 as we predicted.
Part C
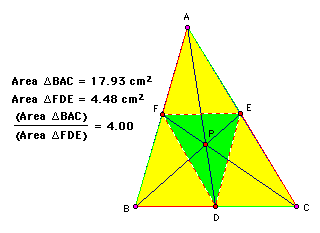
Show that when P is inside ABC, the ratio of the areas of ABC and DEF is always greater than or equal to 4. When is it equal to 4?
First, lets do the construction.
Through observation, the largest area possible of the FED is 1/4 of ABC which occurs when P is the Centroid ABC and FED. If the maximum area of FED is 1/4 of ABC, then it follows that the ratio will be greater than or equal to 4.
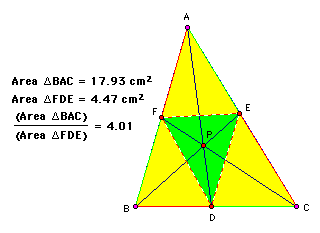
When the ratio = 4 is when P is the Centroid.