Let's explore some graphs!
Here, we are
to graph some equations, and, using what we observe from these
graphs, determine what we think the graphs for ![]() and
and
![]() might look like.
might look like.
Let us begin
by graphing some equations in the form ![]() :
:
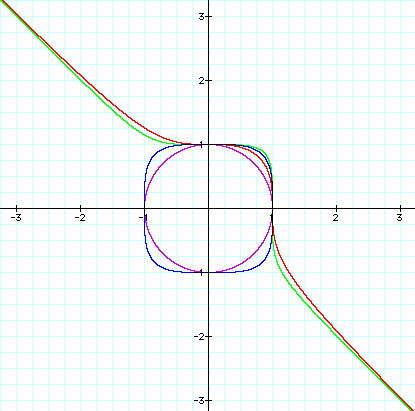
As you can see, depending on whether the exponent n is even or odd, the graph is shaped differently.
Let's first observe the equations with n an even integer.
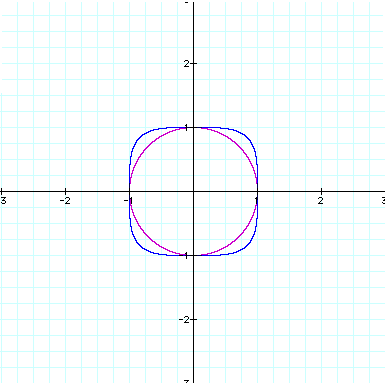
From this, we
can see that if n is even and as n increases, the original circular
shape begins to conform to a square shape. It begins to form "corners".
These corners are getting closer and closer to points (1,1), (-1,1),
(-1,-1), and (1,-1). (This leads me to believe that the equation
![]() will be very much shaped like a
square, with even more defined (closer to 90 degrees) "corners".
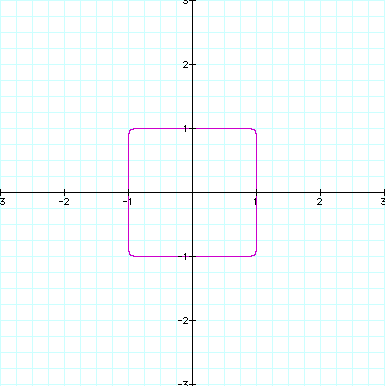
Let's check it out:
will be very much shaped like a
square, with even more defined (closer to 90 degrees) "corners".
Let's check it out:
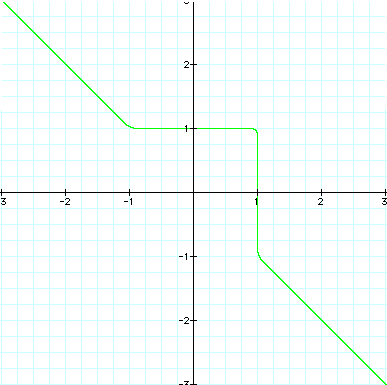
Now let's look at the equations with n an odd integer:
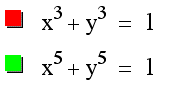
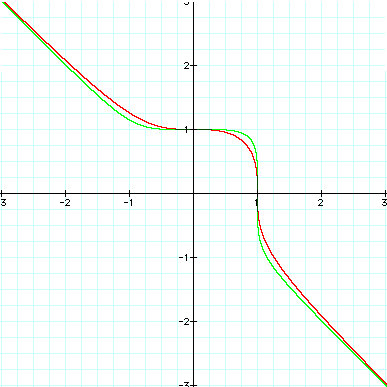
The graph when
n is an odd integer appears to form a graph which curves around
the top right corner of the even integer graphs. When n is odd,
and as it increases, this curve begins to get more square (closer
to 90 degrees) and is getting closer and closer to the point (1,1).
From these obervations, I would guess that the equation ![]() will have the same shape, but the curve will
indeed be closer to (1,1). Let's look and see, shall we!
will have the same shape, but the curve will
indeed be closer to (1,1). Let's look and see, shall we!