Spreadsheet programs such as Excel are excellent programs that can be used to quickly generate a table of values.
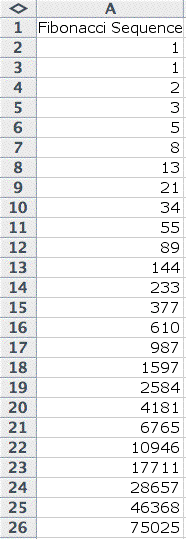
Let's take a look at the Fibonacci Sequence generated using Excel.
| It is easy to see that this sequence gets large very quickly. In order to generate the Fibonacci Sequence, I simply entered the first couple of numbers into A2 and A3. Then, in A4, I assigned the function "=A2 + A3" and then filled down. This generated the sequence I was after. |
 |
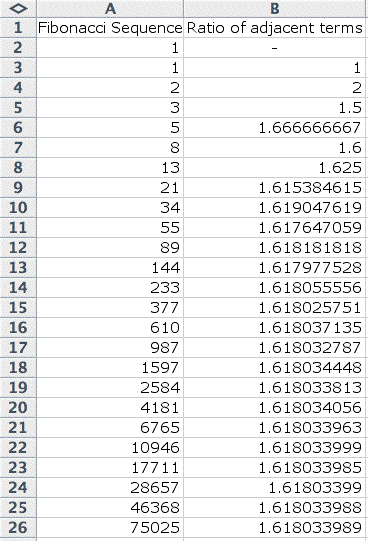
Now, let's explore some ratios within this sequence. Let's look at the ratio of adjacent terms in the sequence.
|
To illustrate this, I just added another column to my data. In this new column, the data consisted of the ratio of the number to the left of it to the number to the left and up one. For example, in B3, I gave the command "=A3/A2" and filled down. Notice that the ratio converges to about 1.618. What does this number represent? The golden ratio, of course! |
 |
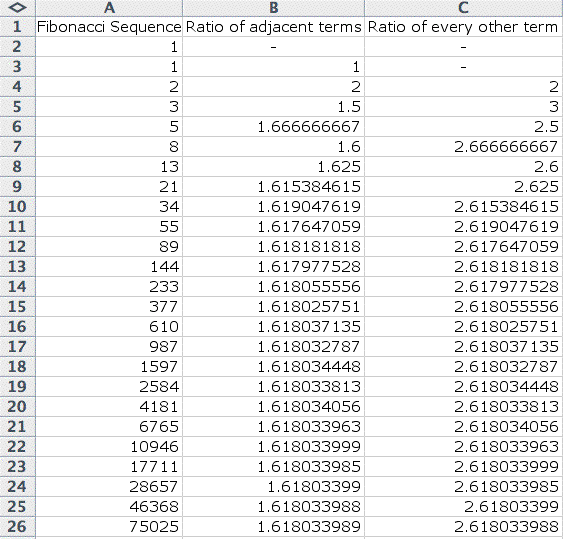
What about the ratio of every other term? Let's add on another column and take a look at these ratios.
|
Beginning in C4, I simply gave the command "=A4/A2" and filled down. Notice that this ratio converges to about 2.618. What is special about this number? How does it relate to the previous ration, the golden ratio? Well, it is the golden ratio squared. |
 |
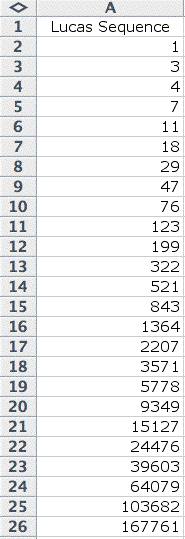
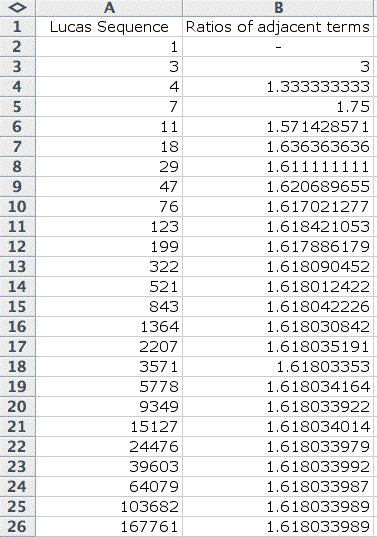
Let's look at another sequence, known as the Lucas Sequence.
| This sequence is similar to the Fibonacci Sequence, but it begins with f(0) = 1 and f(1) = 3. Then f(2) = f(0) + f(1) and so on. So in A4, I gave the command "=A3+A2" then filled down. This gave me the Lucas Sequence. |
 |
What happens if we take the ratios of adjacent terms from this sequence? Let's have a look.
| Here, I used the same command that I used with the Fibonacci Sequence. This ratio also converges to about 1.618, the golden ratio! |
 |