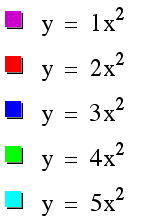
In this assignment, we want to explore the graph of y=ax^2 for different values of a.
Let's first look at how the graph changes when a is different positive integers. We will use y=x^2 as our original graph to compare changes to.
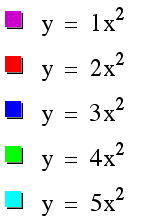
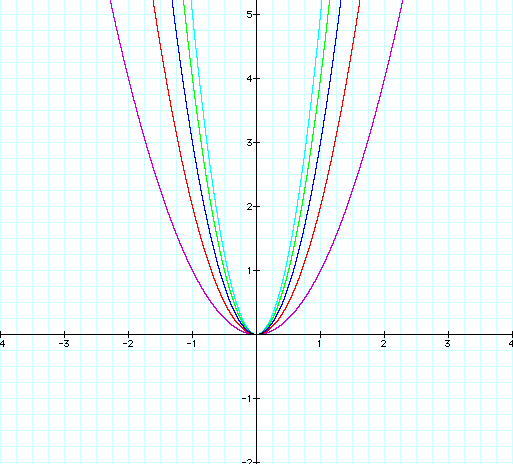
From this illustration, we can see that as a increases, the parabola stretches, or gets thinner. The vertex, however, stays the same.
What happens when a gets closer and closer to 0? Let's take a look (again, let's start with a=1 for comparison):
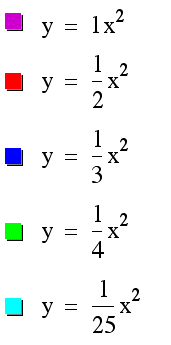
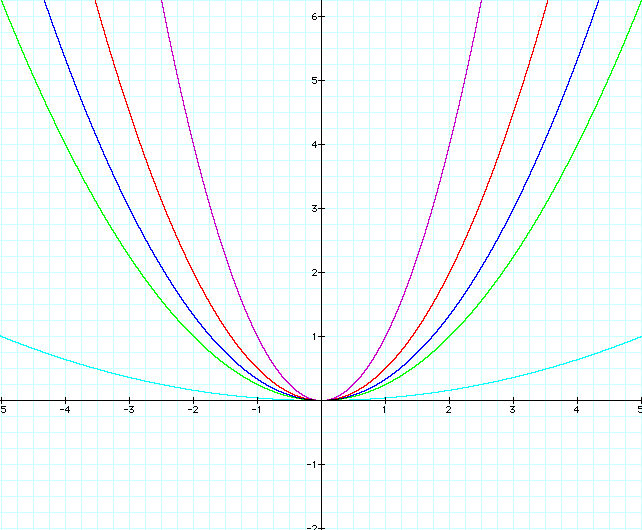
Drawing from this illustration, we notice that as a decreases from 1 and gets closer and closer to zero, the parabola widens, or gets fatter. We should expect this, because if a=0, we just get the line y=x, which is just the x-axis.
So, now that we know what happens with different positive values of a, let's explore negative values of a. For the sake of comparison, let's graph the same values of a, both negative and positive (I have used the same color for both negative and postive values to help us better see the effect.)
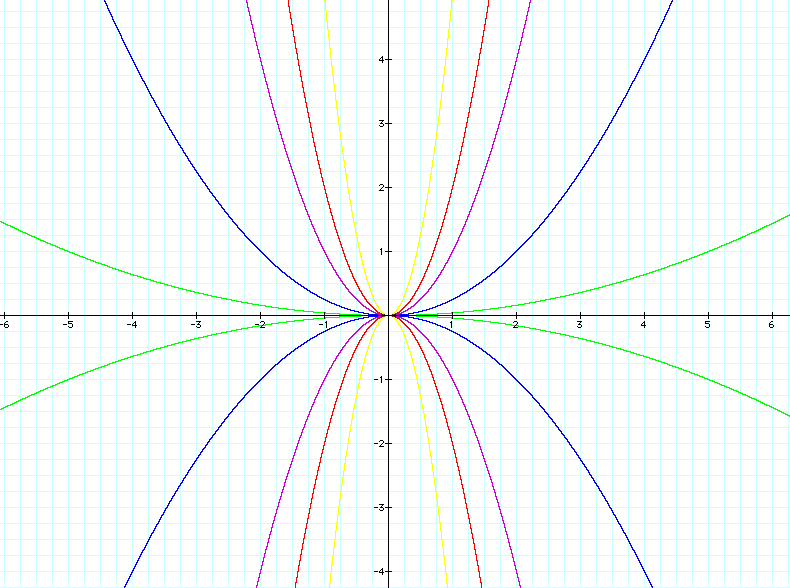
From these graphs, we can easily see that the corresponding negative values of a causes the graph to just reflect about the x-axis. The vertex nor the shape changes; only the way the parabola opens changes.
For fun, and to perhaps better illustrate, click here to see an animation of what has been described above.
In conclusion, changing the value of a in this equation does not change where the vertex is located. As a increases, the parabola gets skinnier, as a decreases, the parabola flattens out, and if a is negative, it is reflected about the x-axis, or it opens downward instead of upward.