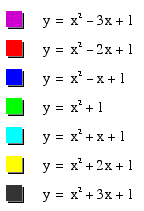
Let's first compare some different graphs of y = x^2 + bx + 1 for different values of b, namely:
b = -3, -2, -1, 0, 1, 2, 3 :
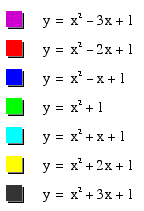
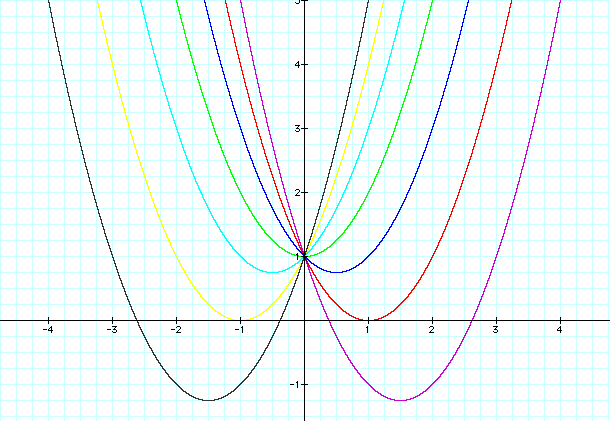
So, how does the parabola move as b is changed?
Well, first of all, notice that the parabola always passes through the same point on the y-axis. With this equation, it is always the point (0,1).
When b < -2, the parabola intersects the x-axis at two positive x values. In other words, the original equation will have two real positive roots.
When b = -2, the parabola is tangent to the x-axis and so the original equation has one real positive root at this point of tangency.
When -2 < b < 2, the parabola does not intersect the x-axis at all. Hence, the original equation has no real roots.
When b = 2, the parabola, again, is tangent to the x-axis. Only, this time, it falls tangent on the negative half of the x-axis, so there is one real negative root.
Finally, when b > 2, the parabola intersects the x-axis twice to show two negative real roots.
Now, let's take a look at just the vertices of each of the graphs above. Do you notice any obvious shape from them?
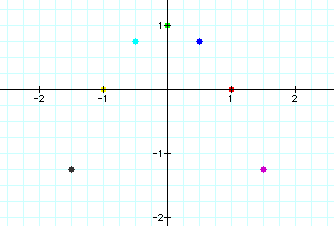
The locus of the vertices appears to form a parabolic shape. Let's take a look at an animation of the equation:
So, the locus of the vertices of our above parabolas create a parabola facing downward with the vertex at (0,1), giving the equation y = -x^2 + 1 :
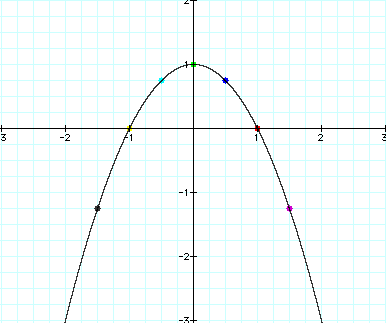
So, in conclusion, given any equation in the form y = ax^2 + bx + c, as b varies while a and c remain the same, the locus of vertices of the parabola will, themselves, form a parabola.