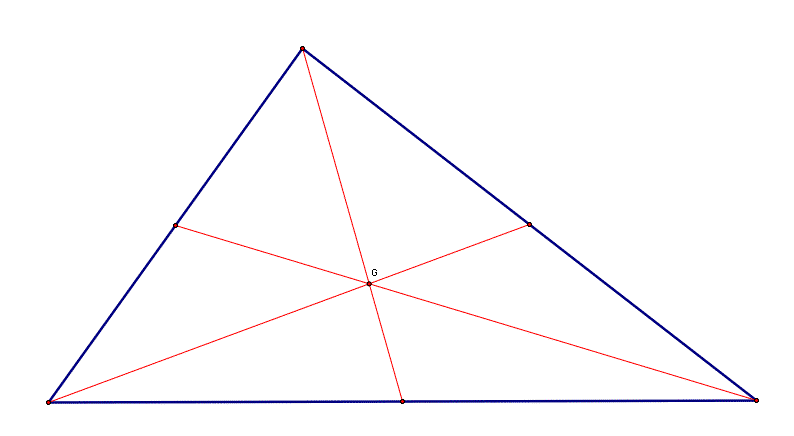
Let's begin by constructing some various centers of triangles.
First, let's look at the centroid of a given triangle. We will call this point G.

The centroid is the point where the three medians intersect. To see how the centroid changes as the triangle varies, click here.
Next, let's look at the orthocenter of the same triangle. We will call this point H.
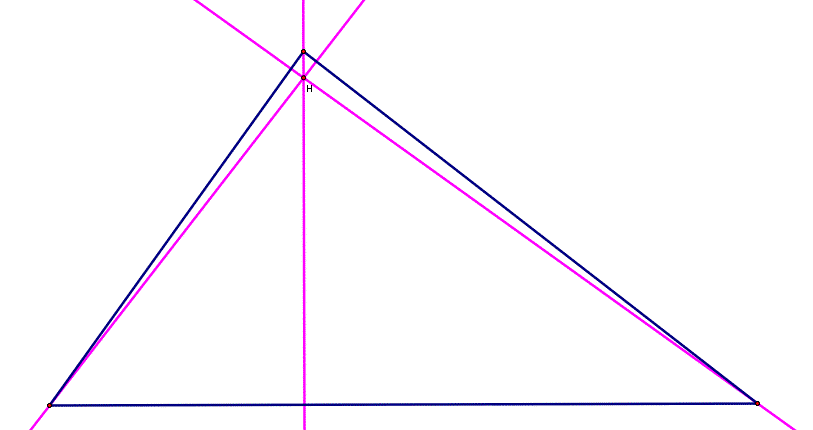
The orthocenter of the triangle is where the three lines containing the altitudes of the triangle intersect. Remember, the altitude is the segment from each of the vertices perpendicular to the side opposite it. To see how the centroid changes as the triangle varies, click here. As you can see, the orthocenter does not always fall in the interior of the triangle.
Next, let's see what the circumcenter of the same triangle looks like. We will call this point C.
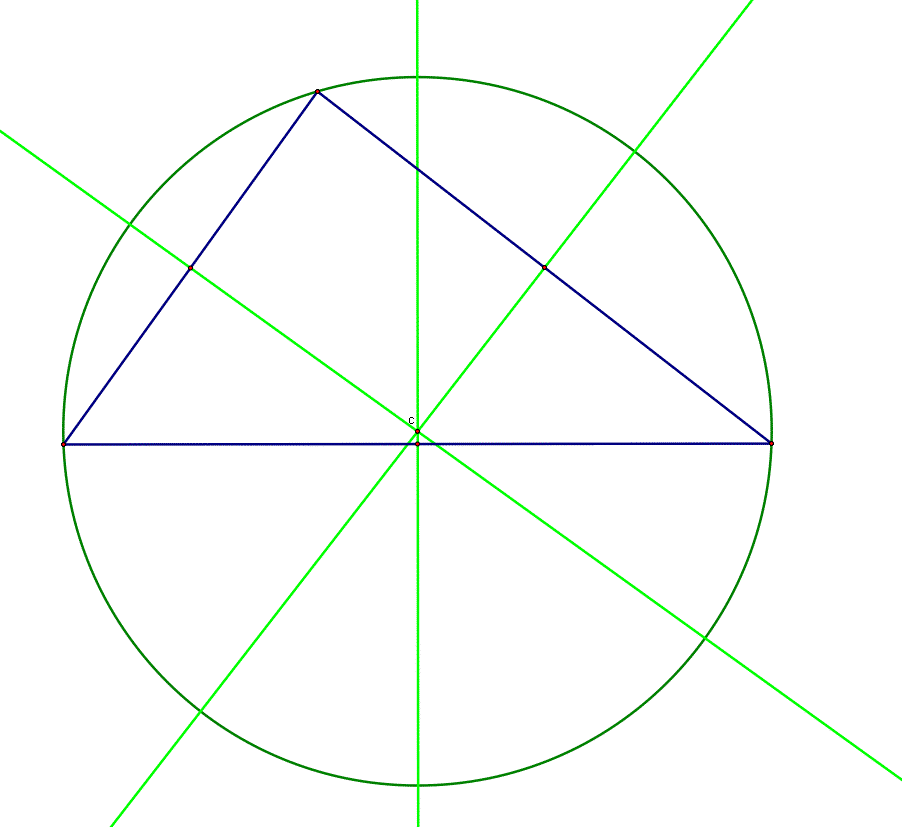
The circumcenter C of a triangle is the point that is the same distance from each of the three vertices of the triangle. C lies on the intersection of the perpendicular bisectors of the sides of the triangle. The circumcircle is the circle that contains the three vertices of the triangle. C is the center of the circumcircle. To see how the circumcenter moves as the triangle changes shape, click here and move the points of the triangle around. Note that the circumcenter may fall outside of the triangle.
Finally, let's take a look at the Incenter of
the same triangle. We will call this point I.
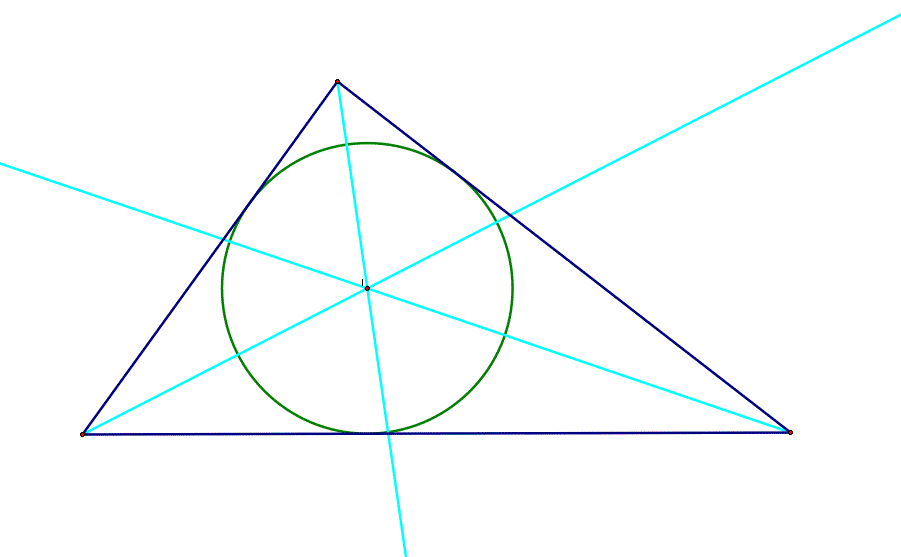
The incenter I of a triangle is the point in the interior of the triangle that is the same distance from each of the three sides. I lies on the intersection of the angle bisectors of each of the angles in the triangle. The incircle is the inscribed circle of the triangle, and its center is the incenter of the triangle. To see how the incenter moves as the triangle changes shape, click here.
Now that we see how each of these centers of a triangle are constructed and what they look like one at a time, let's look at them all together on the same triangle.
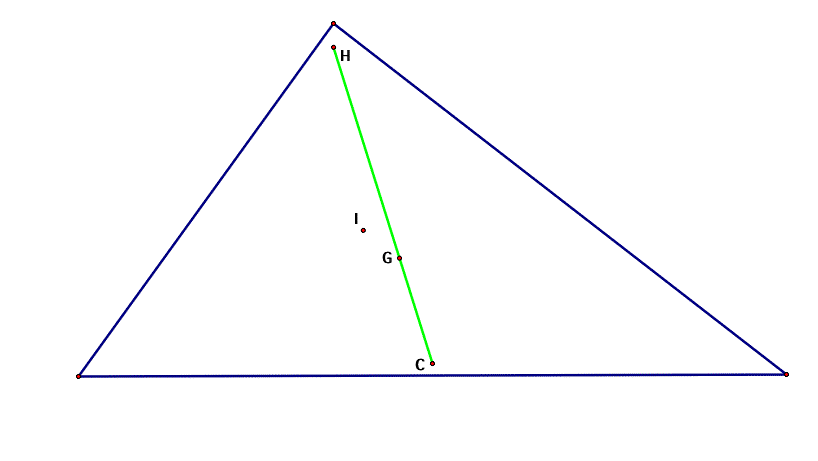
Click here to see how they relate to each other as the triangle changes shape. As you can see from the animation, points H, G, and C have a linear relationship no matter the shape of the triangle.
The medial triangle is the triangle whose sides are made up of the segments connecting the midpoints of the original triangle. It is similar to the original triangle and 1/4 of its area.
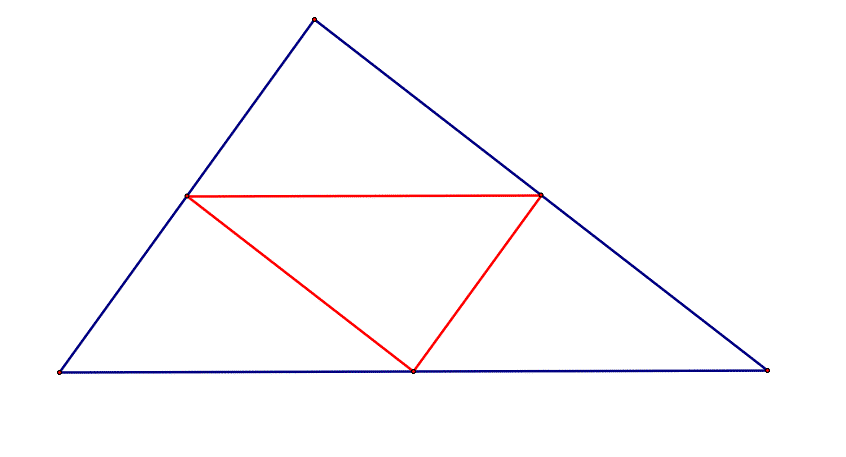
Let's compare the centers of the medial triangle to the centers of the original triangle. Click here to see how the centers relate to each other as the original triangle changes shape. The original triangle's centers will be labeled using capital letters, and the medial triangles centers will be labeled using corresponding lower case letters.
It should be noted that C, G, H and c, g, h all lie on the same segment no matter how the triangle changes. Also, the length from c to h is always half the length of C to H.