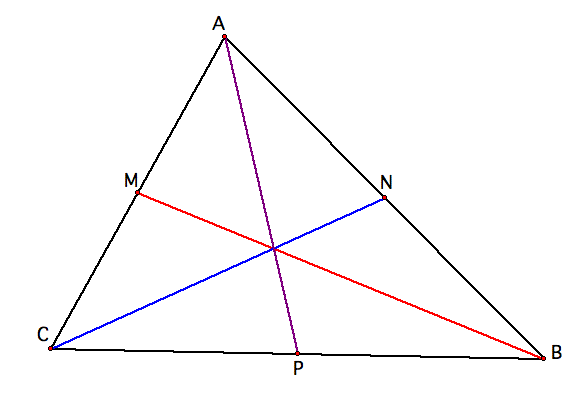
We want to know what the relationship is between a given triangle and a triangle whose sides are made up of the medians of the given triangle.
First, let's construct a triangle and it's medians.

Now, we want to construct a triangle with the three sides having the lengths of these three medians. Let's let MB be one side of this new triangle. To find the other two sides, let's construct some parallel lines. One of these lines should pass through point M and be parallel to CN. The other should pass through point B and be parallel to AP. Let's look at what this looks like:
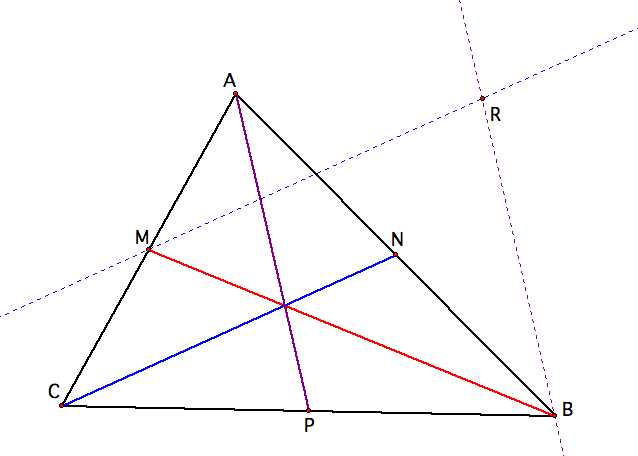
Where these parallel lines cross, we will call this point R. Now, let's construct segments MR and RB so that we may see our new triangle:
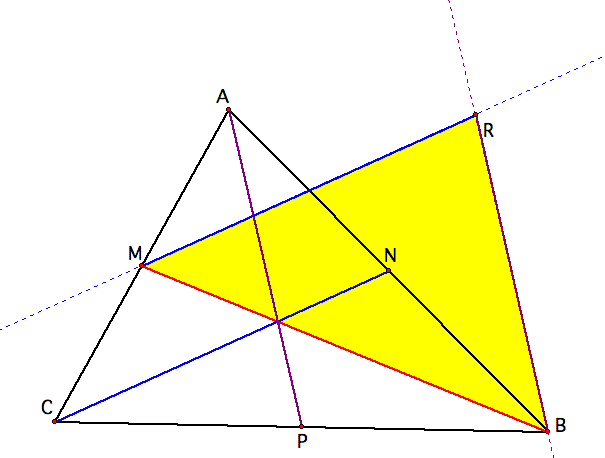
Let's construct the midpoint of MR and call it S.
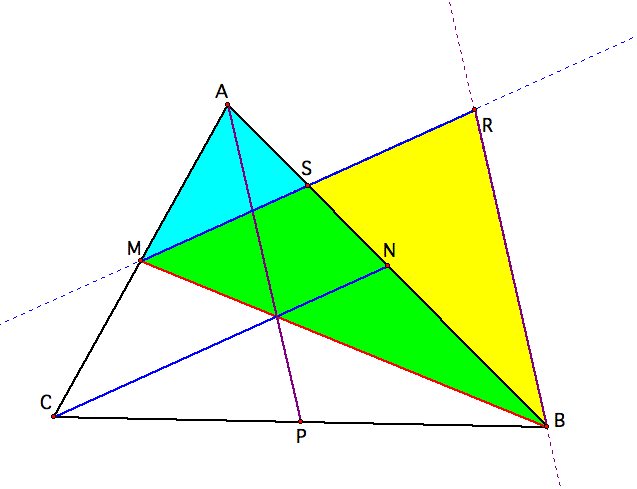
So, BS, which lies on AB is a median of the new (yellow) triangle; BS divides the new triangleMRB in half. Also, notice that MB (a median of the original triangle) divides the original triangle's area in half. How does the left-over (non-overlapped) blue triangle's area compare to the rest of the blue triangle (half of the original area)? Well, it is 1/4 of the 1/2. So, the over-lapped (green) triangle, which is 1/2 of the median triangle is only 3/4 of the whole blue triangle, which is half of the original triangle. So, there is a ratio of the areas of the median triangle to the original triangle of 3:4. Click here to see how the ratio stays the same as the original triangle changes shape.