
In this investigation, we will look at the construction of tangent circles. First, let's look at one circle that is tangent to two given circles.

Tracing the center of the tangent circle, it is plain to see that the locus of the center produces an ellipse. Also, notice that tracing the line that goes through the center of the tangent circle and is also tangent to the ellipse at all times, produces an envelope of lines around the ellipse.
Click here to use the tool to create this type of tangent circle.
Now, let's look at another tangent circle that can be formed with the two given circles.
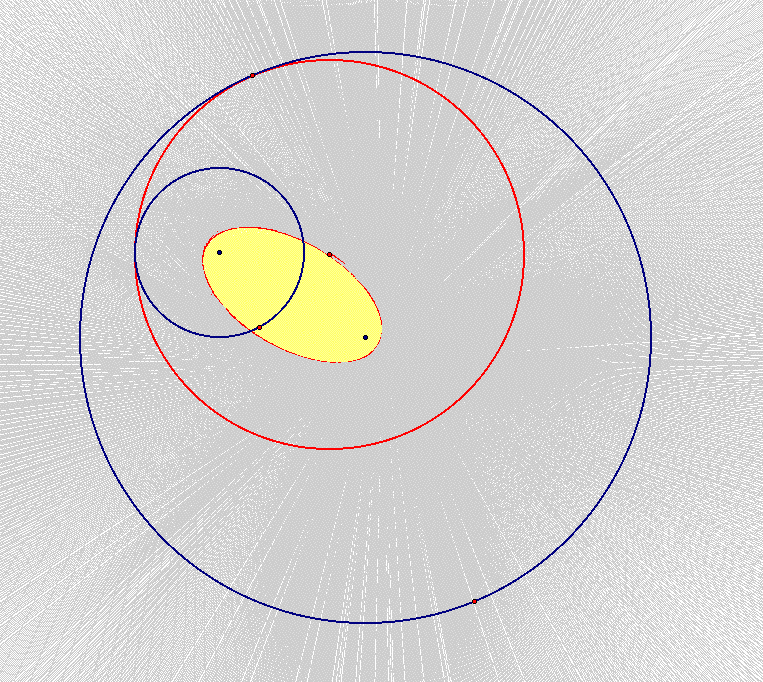
Here, we can see that the locus of the center of the tangent circle also forms an ellipse, and the line tangent to the ellipse passing through the center of the tangent circle forms an envelope of tangent lines.
Click here to use the script tool for this type of tangent circle.
What happens if the given circles intersect? What does the tangent circles look like (depending on whether they are inside or outside), and what does the locus of their centers form?
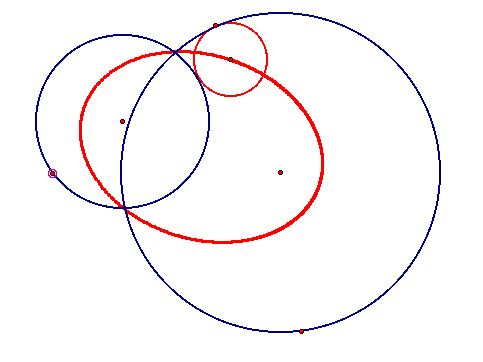

The first image shows the inside tangent circle along with its locus of the center, which appears to form an ellipse. However, the second picture shows the outside tangent circle, and its locus appears to form a hyperbola. Click on the underlined links to play around with the different positions of the tangent circles as you move the given circles around.
The following images show what the tangent circles and their locus look like when the given circles are disjoint.
In each of these cases, it appears that the locus of each tangent circle forms a hyperbola. Again, please click on the links above to play around with the circles for yourself!