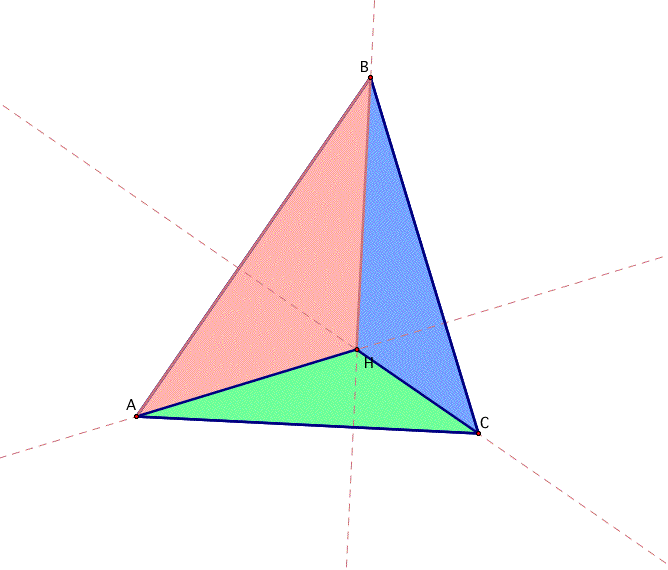
Let's first start off by constructing the orthocenter H of an arbitrary triangle ABC :

Notice that the construction of this orthocenter H divides triangle ABC into three smaller triangles. What happens if we find the orthocenters of these three smaller triangles: AHB, BHC, and CHA?

As it turns out, the orthocenters of the three smaller triangles are acutally the vertices of the large triangle ABC.
Now, let's turn our attention to the circumcircles of all four of these triangles.
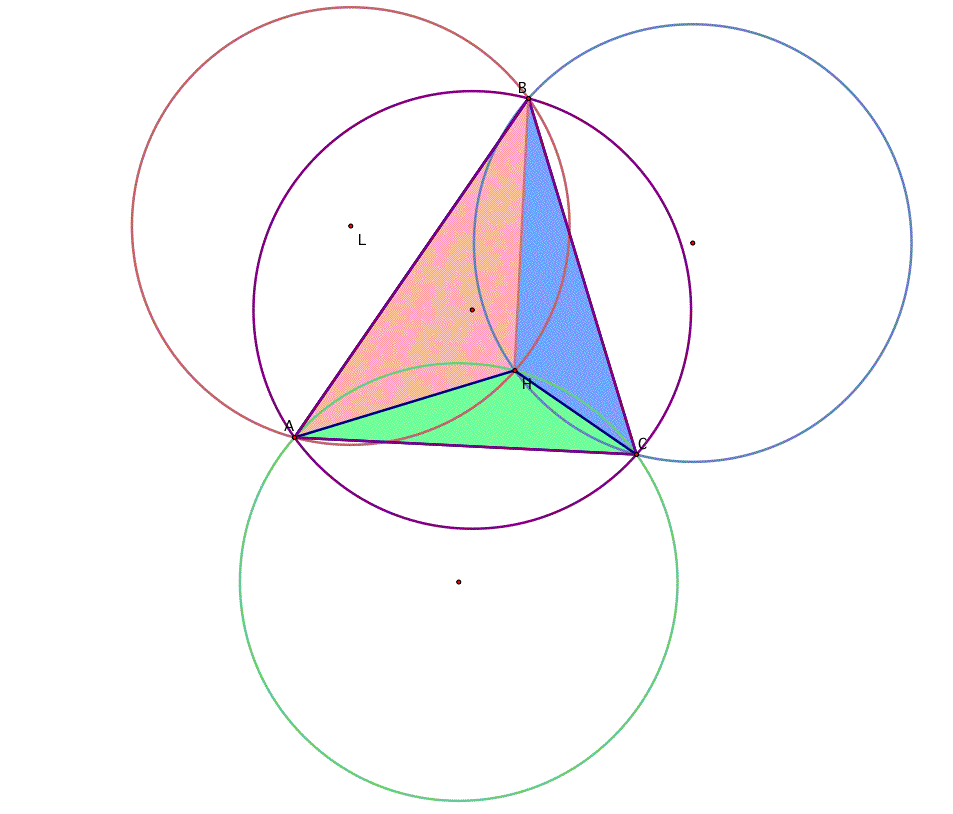
It appears that each of these
circumcircles are the same size. Is this always true? Click here to manipulate the triangles vertices.
What would happen if any vertex of the
triangle ABC moved to where the orthocenter H is located? Where
would H then be located?
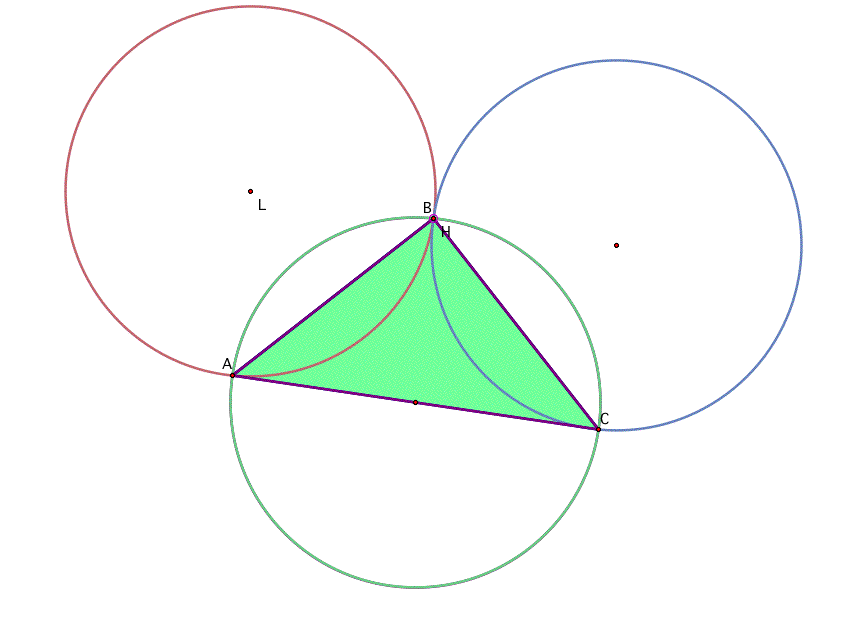
It looks as though the vertex moved becomes H. Click here to try moving different vertices to where H is located.