Assignment 9:

Pedal Triangles

Michelle Greene

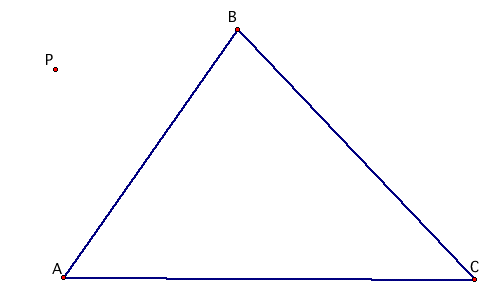
Let's begin by looking at the construction for a pedal triangle.

We will start with a triangle, and pick any arbitrary point P in the plane.

The next step is to construct perpendiculars to the sides of ABC (extended if necessary) and locate the three points R, S, and T that are the intersections.

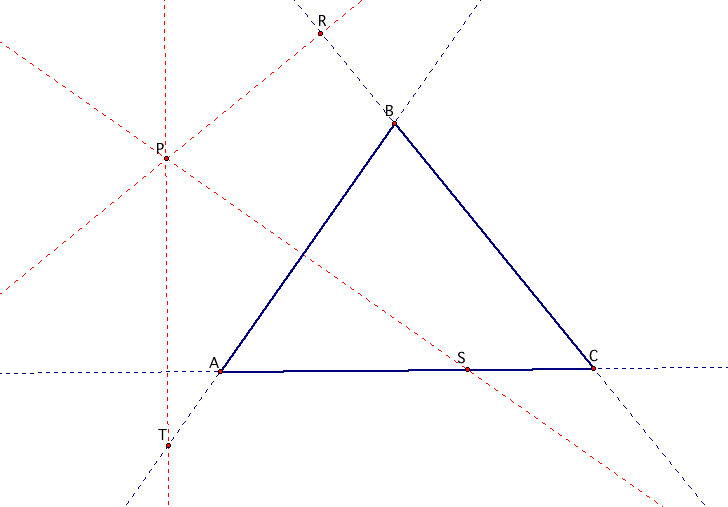
Next, we will connected the points RST to form the pedal triangle. This is the pedal triangle for this particular point P.

Click here to use the script tool to form your own pedal triangle, placing P anywhere in the plane.

Now, let's look at P when it is...

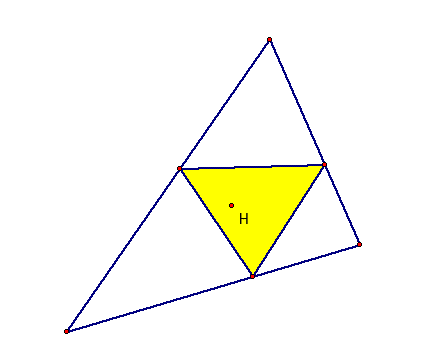
1.) the centroid.

Remember, the centroid is the common intersection of the medians. Let's see what the pedal triangle looks like for the centroid.

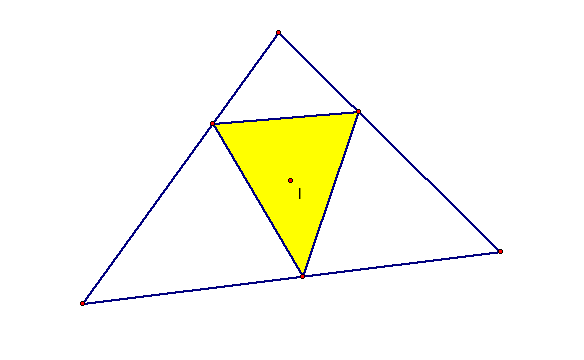
In this case, the vertices of the pedal triangle lie on the sides of the original triangle.

2.) the incenter.

Recall that the incenter of a triangle is the point on the interior of the triangle that is equidistance from all three sides. Let's see what the pedal triangle looks like for the incenter.

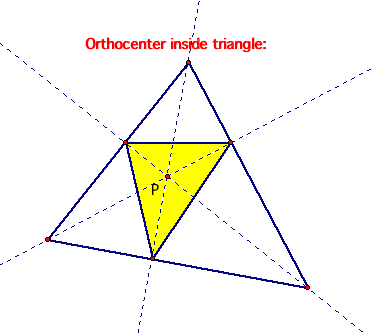
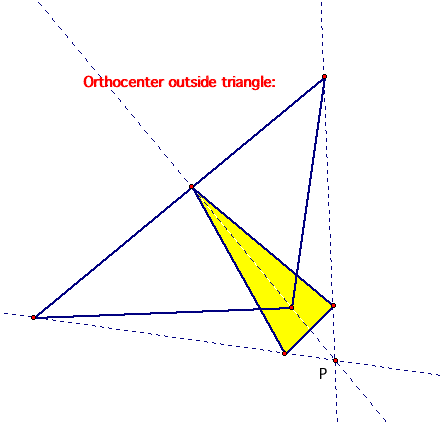
As with the centroid, the vertices of the pedal triangle when P is the incenter will always lie on the sides of the original triangle.

3.) the orthocenter.

Remember that the orthocenter of a triangle is the common intersection of the three lines containing the altitiudes. Let's look at the pedal triangle for the orthocenter when it is inside and outside of the triangle.

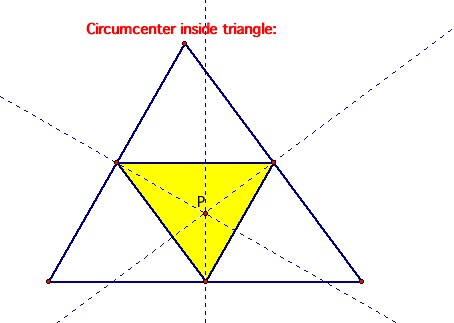
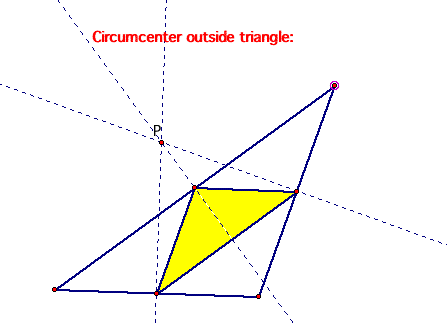
As long as the orthocenter remains inside of the triangle, the pedal triangle remains similar to the previous cases. There is one more thing worth mentioning for this case, however. Notice, that no matter where P is located, the vertices of the pedal triangle remaing on the altitudes of the original triangle.

 

4.) the circumcenter.

The circumcenter of a triangle is the point in the plane equidistance from the three vertices of the triangle. Let's look at the pedal triangle for the circumcenter when it is inside and outside of the triangle.

This case looks pretty similar to the orthocenter case. However, in this case, the vertices of the pedal triangle always lie on the perpendicular bisectors of the original triangle.

5.) on one of the sides of the triangle.

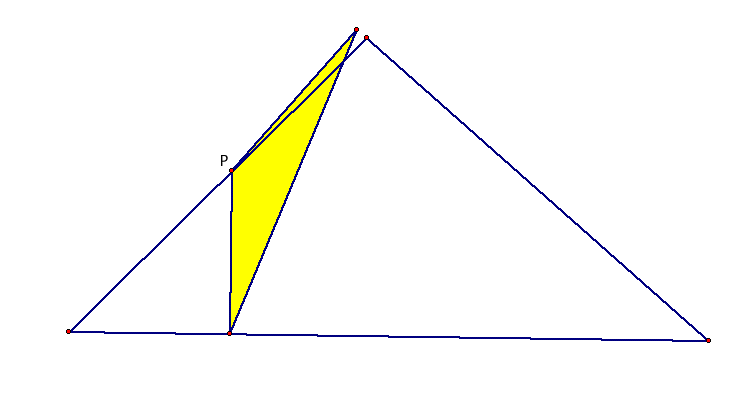
When P lies on one of the sides of the original triangle, P actually become one of the vertices of the pedal triangle.

6.) one of the vertices of the triangle.

 

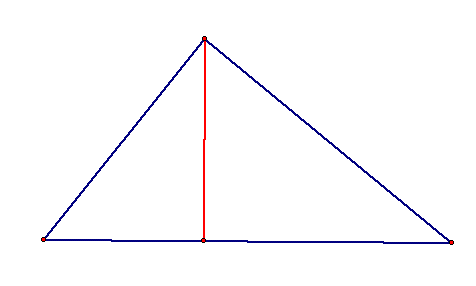
Your initial thought may be to say that there is no pedal triangle for this case. However, this is actually a special case. In this case, the three vertices of the pedal triangle are colinear. This is also known as a degenerate triangle. The line segment formed (the red segment above) is called the Simson Line.

Are there any other cases for which the Simson Line exists? What if P lies on the circumcircle? Click here to see the animation of P as it rotates around the circumcircle.

As you can see, if P lies anywhere on the circumcircle of the original triangle, then the pedal triangle formed will always be the Simson line.

 

 

Return