Our task is to consider any triangle ABC and select a point P inside the triangle. We are to draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively. Our triangle should resemble the following:
Next, we are to explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P.
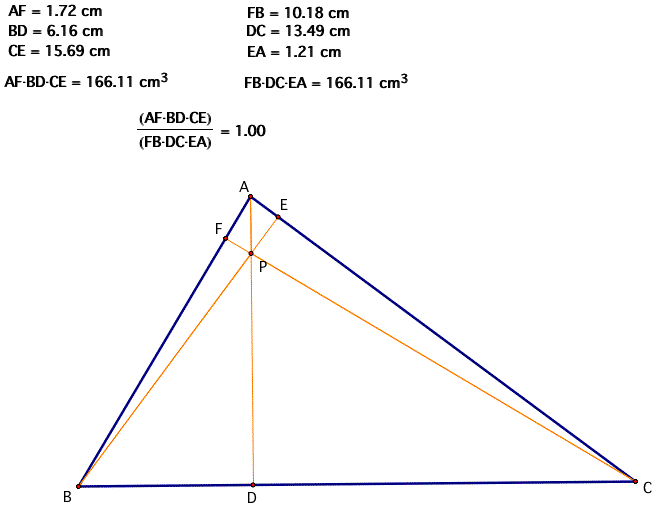
To start us off, let's take triangle ABC and look at point P as the orthocenter. What are the relationships of these segments?

For this particular triangle, it appears that (AF)(BD)(EC) and (FB)(DC)(EA) are equal, therefore, the ratio of (AF)(BD)(EC) to (FB)(DC)(EA) is equal to 1.
What happens as this triangle changes shape? Click here to see the triangle vary. As you can see when P as the orthocenter remains inside of the triangle, this ratio remains 1. i.e., (AF)(BD)(EC) and (FB)(DC)(EA) remain equal.
What about P as the circumcenter? What are the relationships of the same segments?
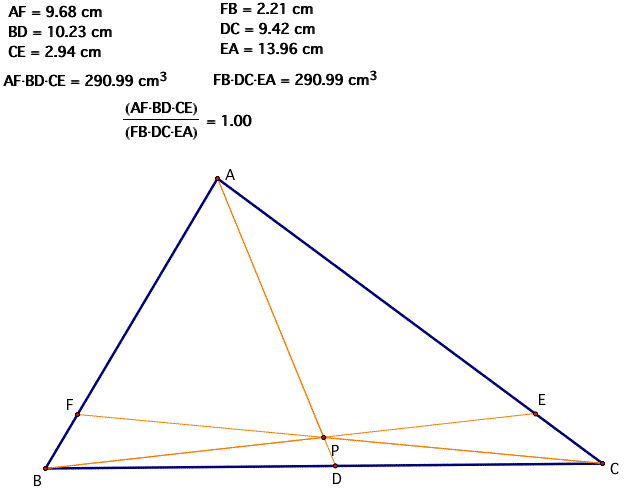
Again, it appears as though when P is the circumcenter, (AF)(BD)(EC) and (FB)(DC)(EA) are equal, therefore, the ratio of (AF)(BD)(EC) to (FB)(DC)(EA) is equal to 1.
Click here to see this triangle vary, keeping P (the circumcenter) on the inside. As you can see, as long as P, the circumcenter, remains inside the triangle, this ratio remains equal to 1.
Let's look at another center, the incenter. Let's take a look at these same relationships when P is the incenter.
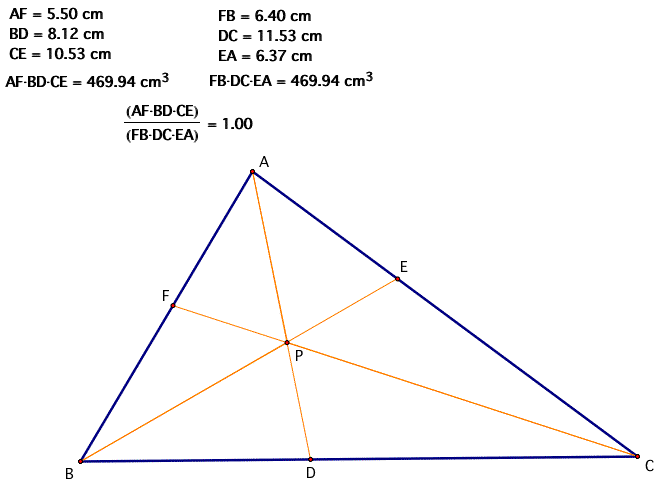
It looks as though we get the same result. Click here for the animation of triangle ABC which keeps P, the incenter, on the inside. Once again, the ratio remains 1.
The final center I would like to address as point P is the centroid. Let's take a look once more at these relationships when point P is the centroid.
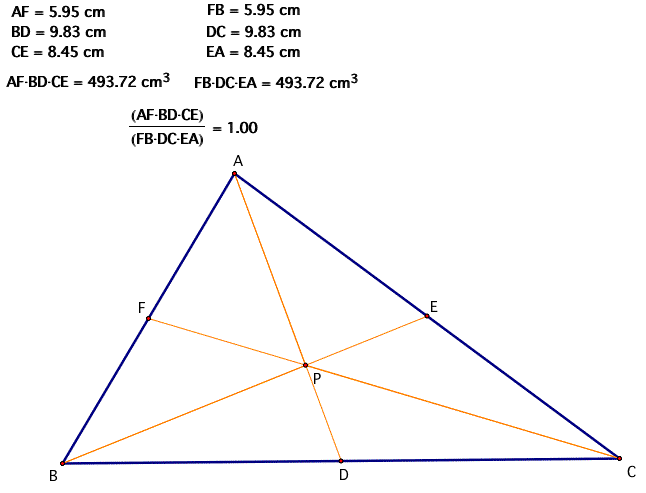
Once again, we get the same results when P is the centroid. Click here to see this animation.
Finally, click here to animate point P anywhere inside the triangle to see that the ratio of (AF)(BD)(EC) to (FB)(DC)(EA) is always equal to 1.
How do we know that this ratio is always equal to 1? Let's first look at some similar triangles and the ratios they produce.
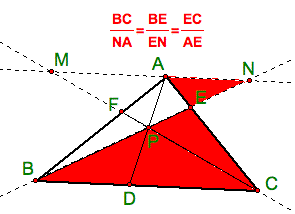
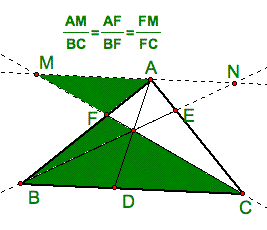
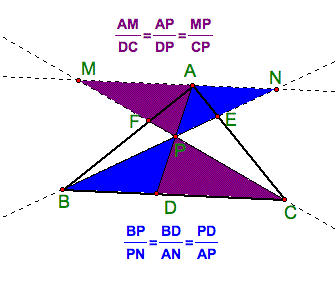
What we want to prove is that:
Let's rewrite the equation as follows:
Now, all we need to do is substitute in using the proportions we came up with above using similar triangles:
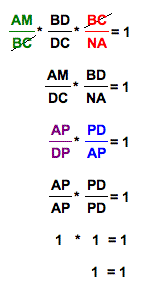
So, this ratio is always equal to 1.
Here's another question: Can this result be generalized (using lines rather than segments to construct ABC) so that point P can be outside the triangle? Click here to see what happens. The ratio still remains 1 !!
When P is inside the triangle, what is the ratio of the areas of triangle ABC and triangle DEF?
Click here to enter GSP. Click and drap point P anywhere inside the triangle. What do you notice about the ratio? You should see that the ratio is always greater than or equal to 4. Can you position P so that the ratio is exactly 4?
When is the ratio 4? Look at the ratio when P is the centroid and ABC is any triangle. Click here to see an animation.