Let's first start off with the definition of a continuous function, then we will proceed through some problems that are designed to assist in the development of a greater conceptual understanding of the concept of a continuous function.
A function f is continuous at x=a provided all three of the following are truc:
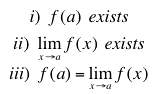
In other words, a function f is continuous at a point x=a, when (i) the function f is defined at a, (ii) the limit of f as x approaches a from the right-hand and left-hand limits exist and are equal, and (iii) the limit of f as x approaches a is equal to f(a).
Before we go further, let's begin by constructing functions that are not continuous. For each of the following, sketch a graph of a function that is not continuous at x=2 when:
a) (i) is true, but (ii) is false.
b) (ii) is true, but (i) is false.
c) (i) and (ii) are true, but (iii) is false.
Now, let's us consider the graph of a function f below.
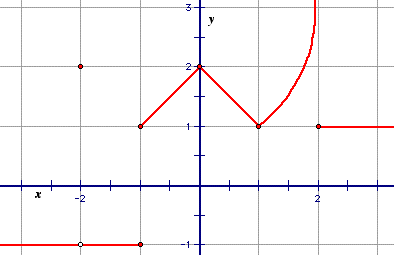
For what numbers x in [-3, 3] is f not continuous at x?
Next, let's try our hand at another function. For some non-zero number a, define
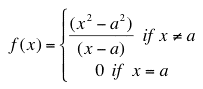
a) Is f defined at a?
b) Does
exist?
c) Is f continuous at a?
Now, for a bit more complicated problems. If 
,
which of the following statements, if any, must be true?
a) f is defined at a.
b) f(a)=L
c) f is continuous at a.
Consider the next function,
Now, (1) find all values of a and b such that f is continuous at x=1 and (2) draw the graph of f when a=1 and b=-1.
As we begin to develop a better understanding of continuity, determine whether the following statements are always true or sometimes false. Be sure to justify your answers with an example.
a) If f(1)<0 and f(2)>0, then there must be a point p in (1, 2) such that f(p)=0.
b) If f is continuous on [1, 2], f(1)<0 and f(2)>0, then there must be a point p in (1, 2) such that f(p)=0.
c) If f is continuous on [1, 2] and there is a point p in (1, 2) such that f(p)=0, then f(1) and f(2) must have different signs.
d) If f has no zeros and is continuous on [1, 2], then f(1) and f(2) have the same sign.
And, for those of you who love traveling problems: John takes a trip from Portland, OR to Seattle, WA. He leaves at 8:00 am on Monday and arrives at 12:00 pm that same day. He returns on Tuesday, leaving Seattle at 8:00 am and arriving back in Portland at 12:00 pm, retracing exactly the same route. Show that there is a point on the road through with he passes at the same time both days.
This activity was adapted from a Math Excel course taught at Portland State University, spring term 2004 by Joe Ediger and Erin Horst.