For this activity, we will not begin by rattling off definitions, but work through an activity that will leave you with a general understanding of the concept of derivative. After completing the activity, definitions will be provided.
For this activity, you will need the geometric software program, Geometer's Sketchpad (GSP). Before we can begin exploring, you will need to download this GSP file copyright by Scher, Steketee, Kunkel, & Lyublinskaya, 2005.
To begin, open the GSP file, Instantaneous Rate.gsp. You should have an opend sketchpad that looks like the following.
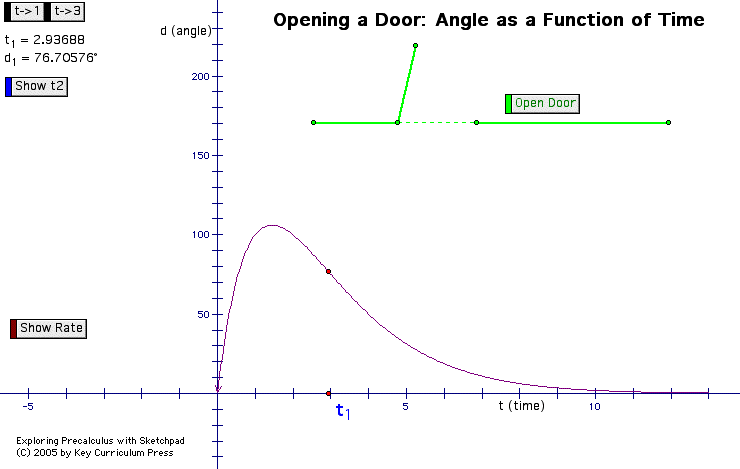
This activity will explore the angle of an automatic door (d) as function of time (t). Before going further, press the"open door" button to operate the door. Watch the movement of the point t1 as the door opens and closes. You can also manipulate the point t1 youself, by dragging it back and forth along the t-axis.
As you observe the movement of the door, what happens to the values of t1 and d1? For what values of t1 is the door opening, or the angle incresing? For what values of t1 is the door closing, or the angle decresing? What is the time when the door is open to its fulles? How do you know this value?
Next, we would like to find the rate of change of the door's
angle, but we will need another point. To show t2, press the "show
t2" button. Now, drag t1 across the t-axis and observe
the behavior of t2. What happens to t2 as you change 
?
(Note that the value of 
is the distance
between t1 and t2). What happens to the values of t2 and d2 as
becomes smaller? What happens when you move
the slider value of t2?
Using 
set to 0.1, calculate the rate
of change of the door's angle for any time t, usign the
values t1, t2, d1, and d2. You can use GSP to perform this calculation
for you. What can you say about the door's motion from the rate
of change? Now, press the "show rate" button. What does
the dotted line represent? What is the dotted line's relationship
to your calculate rate of change? When you move the point t1 along
the t-axis what happens to the dotted line? Can you tell
when the door is opening and closeing and the door's rate from
the dotted line?
Now, set 
and t1=1. What is the rate of change
at that time?
Next, select the values t1, d1, t2, d2, ,
and the rate of change (in that order on the left hand side of
the sketch), then choose Tabulate from the Graph menu. Once the
table has been constructed, double click the first entry to make
it permanent.
Now, change 
to .01 and notice
values change in the table. Double click the table values to make
them permanent. What happens to the rate of changa as values of
change? Perform the previous action of changing
values of and record the subsequent values
within the table. What occurs to the rate of change as the value
of becomes smaller?
Next, using the button "t->3", which represents
the value of t1 at 3 seconds, record the values of as
it runs through the values .1 to .000001. What happens?
To proceed further, note that the rate of change is the rate of change between two different values of t, while the instantaneous rate of change is the exact rate of change at one specific time, t. Now, since we need two values to compute the rate of change, we can calculate the instantaneous rate of change by making our two values 'close' to each other. To do this, we can take the limit of the rate of change as the second value, t2, approaches the first, t1. Now, as you may or may not have guessed, the instantaneous rate of change is the derivative of the function, that is, the limit of the average rate of change as the interval between t1 and t2 gets closer and closer to zero. Now, what is the derivative of the door's angle when t1 is 1 second (use the "t->1" button)?
To conclde the activity, take a few minutes to write down your own definition of the derivative of a function.
This activity was adapted from Scher, D., Steketee, S., Kunkel, P., & Lyublinskaya, I. (2005). Exploring precalculus with The Geometer's Sketchpad. Emeryville, CA:Key Curriculum Press.
Now that we have an idea of what the derivative of a function is, consider the following mathematical definition:
The derivative of a function f at a number a, denoted by f'(a), is
(Stewart, 1998).Or, an equivalent definition, is
(Stewart, 1998).However, what benefit is this above definition, if we do not know what a derivative is in layman's terms. The most basic way to describe the derivative in one simple term is "slope" (Adams, Hass, & Thompson, 1998). Consider the following illustration from How to Ace Calculus: The Streetwise Guide (Adams et al., 1998), to illustrate this concept further:
Let us suppose you have a tranquilized goat, which you are going to carry up a hill. If you begin at the base of the hill, let's say coordinates x=0 and y=0, and climb up the hill, both your x and y coordinates will increase. If we let h(x)=y be the function that defines the hill you are walking up, then the derivative of h(x), is exactly the steepness of the hill at some point x, denoted h'(x). Now, consider for example h'(10)=1/6, that is, after reaching10 feet in the x direction, you are at a point where the steepness is 1/6. This means that for every foot you travel horizontally, along the x axis, you must travel 2 inches in the verical direction, or along the y axis. This is not that steep of an incline. However, if h'(20)=5, this means that for every 1 foot you travel horizontally, along the x axis, you must travel 5 feet vertically, along the y axis. This is quite steep and may require extensive mountainering equipment. Now, if h'(40)=-3, this would mean that when x=40, you are heading in a negative direction, that is for every 1 foot in the horizontal direction, you are going downhill 3 feet. At this point it will not be necessary to carry the goat on your back, but rather roll it down the hill.
Now, consider the following two simple facts about derivatives:
,
where 
.
where
a is a fixed value. If we want a to vary, or change,
we will replace a by x, giving 
.
Using this latter function, we can assign x to the number
f'(x), creating a new function, called the derivative
of f.
Adams, C., Hass, J., & Thompson, A. (1998). How to ace Calculus: The streetwise guide. New York: W. H. Freeman & Co.
Stewart, J. (1998). Calculus: Concepts and contexts. Pacific Grove, CA: Brooks/Cole Publishing Co.