Now that we have explored derivatives, we can now progress to the rules of differentiation. These rules are simply formulas that instruct the learner how to compute derivatives depending on a given function.
The most complex (and useful) rule of differentiation is the chain rule. The rule states, that if f and g are both differentiable and F=f(g(x)), then F is differentiable and F' is given by the product F'(x)=f'(g(x))g'(x) (Stewart 1998).
To illustrate the chain rule, consider the following functions and their respective derivatives. It is suggested that you compute the derivative to verify the function of the derivative.
The follwing graph illustrates the function 
and its derivative 
.
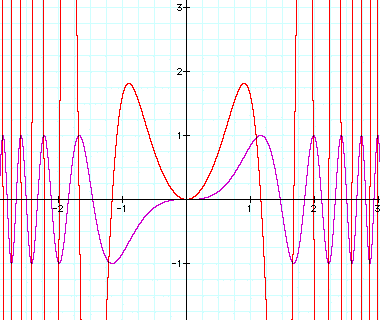
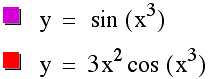
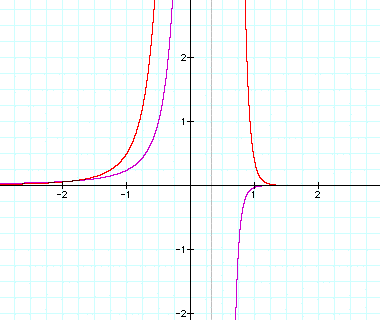
The following graph illustrates the function 
and its derivative 
.
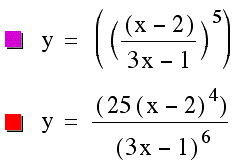
For additional practice with the chain rule, compute the derivatives for the following functions:
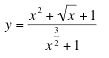
The above problems were adapted from a Math Excel class instructed by Joe Ediger and Erin Horst.
Stewart, J. (1998). Calculus: Concepts and contexts. Pacific Grove, CA: Brooks/Cole Publishing Co.