

Make up linear functions f(x) and g(x). Explore, with different pairs of f(x) and g(x) the graphs for
i. h(x) = f(x) + g(x)
ii. h(x) = f(x)g(x)
iii. h(x) = f(x)/g(x)
iv. h(x) = f(g(x))
Summarize and illustrate
Let's begin our exploration with f(x) = x and g(x) = x+1. Then,
i. h(x) = (x) + (x+1)
ii. h(x) = (x)(x+1)
iii. h(x) = x/(x+1)
iv. h(x) = (x+1)
And the graph is:
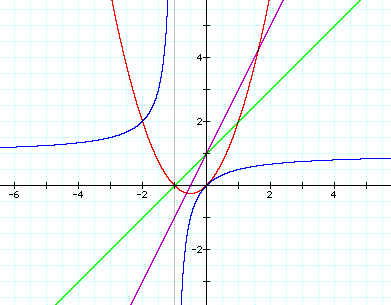
Next, let us consider f(x) = 2x+ 3 and g(x) = -4x + 1
i. h(x) = (2x + 3) + (-4x + 1)
ii. h(x) = (2x + 3)(-4x+1)
iii. h(x) = (2x + 3)/(-4x+1)
iv. h(x) = 2(-4x+1) + 3
And the graph is:
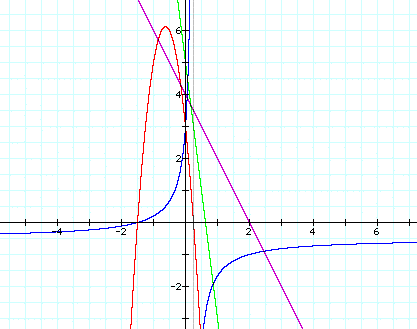
Lastly, let us consider f(x) = (1/2)x and g(x) = (-2/3)x + 1
i. h(x) = (1/2)x + ((-2/3)x + 1)
ii. h(x) = ((1/2)x)((-2/3)x + 1)
iii. h(x) = ((1/2)x)/((-2/3)x + 1)
iv. h(x) = (1/2)((-2/3)x + 1)
And the graph is:
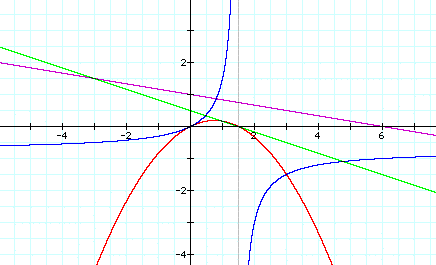
Now, we can infer conclusions of two linear functions, f(x) and g(x), when they are added, multiplied, divided, and composed together.
When we have two linear function, f(x) and g(x), added together we know their sum will result in a linear function. For example, consider when f(x) = x and g(x) = x+1, then h(x) = f(x) + g(x) = (x) + (x+1) = 2x + 1. This occurs since we are only adding quantities of x to each other (i.e. 5x + 2x = 7x). It is also important to recall that we can have negative slopes for our linear functions f(x) and g(x) if:
Next, when we multiple two linear functions, f(x) and g(x), together we know their sum will result in a quadratic function. For example, consider f(x) = x and g(x) = x+1, then h(x) = f(x)g(x) = x(x+1) = (x^2) + x. This occurs since we are multiplying two single powers of x together (i.e. (x)(2x) = 2(x^2)). It is important to note that when we multiply two negative values of x together we get a positive slope, two positive values of x together we get a positive slope, and a positive x multiplied by a negative x will result in a negative slope of the quadratic equation.
When we divide two linear functions, f(x) and g(x), together our result is a rational function. Recall, a rational function is a function in which a polynomial function is divided by another polynomial function, such as h(x) = f(x)/g(x). Consider the example f(x) = x and g(x) = x+1, then h(x) = f(x)/g(x) = x/(x +1). It is important to note again that the "rules" of multiplying or dividing negative and positive numbers will either result in a positive or negative slope for the rational function h(x).
Lastly, when we composite two functions, f(x) and g(x), together our result will be a linear equation. For example, consider f(x) = x and g(x) = x+1, then h(x) = f(g(x)) = (x +1). This occurs since we are substituting the variable x within the linear function f(x) by the linear function g(x), which provides a resulting linear equation. As above, the "rules" of multiplying negative and positive numbers together will either result in a positive or negative slope of the resulting linear equation.