

Investigate each of the following for
Describe each when a = b, a < b, and a > b.
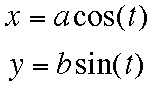
Let's begin by examining
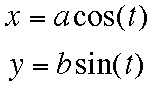
For values of
where a = b, a < b, and a > b.
First, consider when a = b = c where c is some constant.
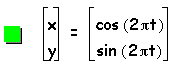
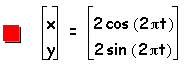
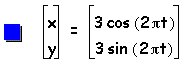
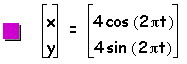
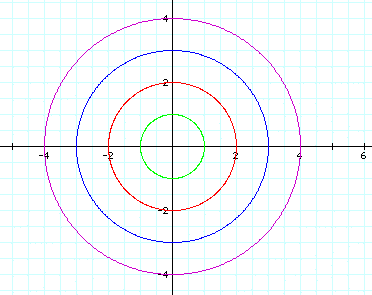
Through examination of the parametric curve we can determine that when a=b=c where c is a constant, then the parametric curve will be a circle with x and y intercepts at c and -c.
Next, let us examine the same parametric equations, but when a < b, where a=1 and b=2, 3, 4, 5. Then the graph of the curve is
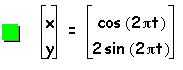
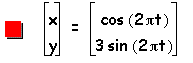
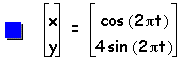
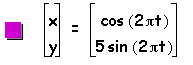
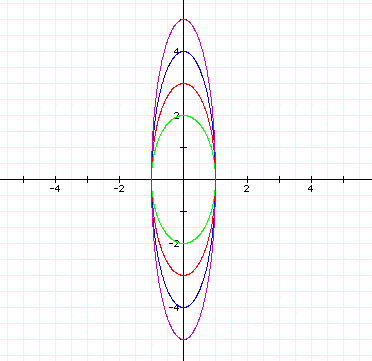
Now, through examination of the above parametric curve, we can determine that when a < b that the curve will be an ellipse whose major axis is on the vertical y-axis and minor axis is on the horizontal x-axis. Additionally, the x-intercepts will be 1 and -1 (or a and -a) and the y-intercepts will be b and -b.
Next, let us consider when a > b for the same parametric equations with b=1 and a= 2, 3, 4, 5. Then, the graph of the curve is
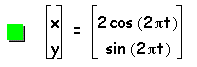
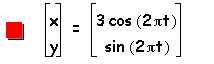
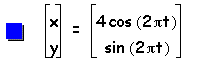
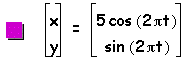

Then, through examination of the parametric curve we then determine that when a > b that the curve will be an ellipse whose major axis is on the horizontal x-axis and minor axis on the vertical y-axis. Additionally, the y-intercepts will be 1 and -1, or b and -b, and the x-intercepts will be a and -a.