

Let triangle ABC be any triangle. Then if P is any point in the plane, then the triangle formed by constructing perpendiculars to the sides of ABC (extended if necessary) locate three points R, S, and T that are the intersections. Triangle RST is the Pedal Triangle for Pedal Point P.
Explore point P when it is a 'special' point of triangle ABC and discuss.
Let us explore constructions of the pedal triangle RST when pedal point P is 'special' points of triangle ABC (i.e. centroid, othrocenter, incenter, circumcenter, vertice) and on a side.
Let us begin with pedal triangle RST with pedal point P where P is the centroid of triangle ABC.
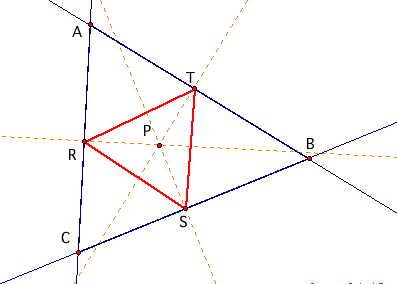
When we adjust triangle ABC we see that pedal triangle RST is always inside triangle ABC or it is a Simson line. A Simson line occurs when the three vertices of the pedal triangle RST are collinear (RST is a degenerate triangle). To adjust triangle ABC yourself, download the GSP file.
Next, consider pedal triangle RST with pedal point P where P is the orthocenter of triangle ABC.
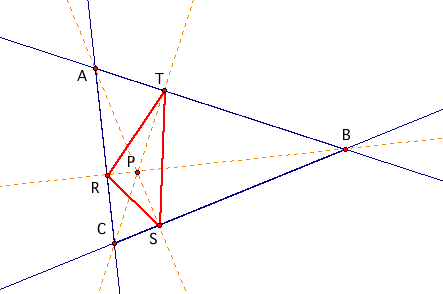
When we adjust triangle ABC we see that pedal triangle RST can be inside or outside ABC or a Simson line. To adjust triangle ABC yourself, download the GSP file.
Now, consider pedal triangle RST with pedal point P where P is the incenter of triangle ABC.
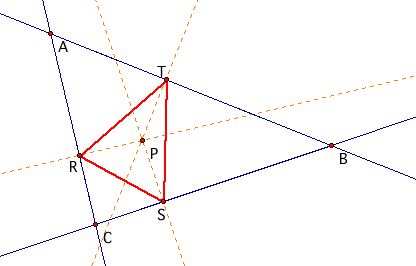
When we adjust triangle ABC we see that pedal triangle RST is always inside triangle ABC. To adjust triangle ABC for yourself, download the GSP file.
Now, consider pedal triangle RST with pedal point P where P is the circumcenter of triangle ABC.
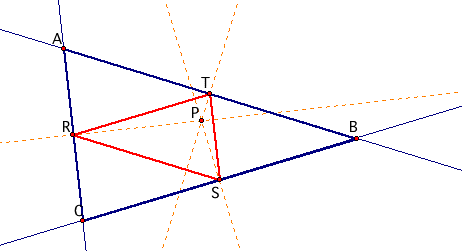
When we adjust triangle ABC we see that pedal triangle RST is always inside triangle ABC. To adjust triangle ABC for yourself, download the GSP file.
Now, consider pedal triangle RST with pedal point P where P is one of the vertices of triangle ABC.
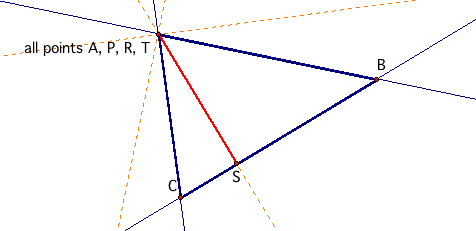
When we adjust triangle ABC we see that pedal triangle RST is always a Simson line and never a triangle by construction. To adjust triangle ABC for yourself, download the GSP file.
Now, consider pedal triangle RST with pedal point P where P is on one side of triangle ABC.
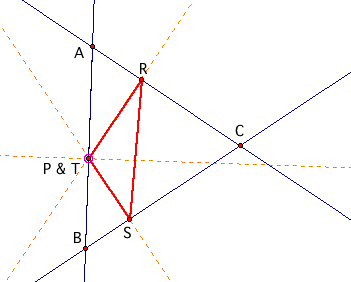
When we adjust triangle ABC we see that pedal triangle RST is either a triangle inside triangle ABC or a Simson line. To view an animation with P moving along side AB, download the GSP file.