This task provides a geometric representation of the derivative of the product of two functions. After constructing the model, the learner can derive the formula for the Product Rule.
Supplies you will need:
The Product Rule: If 
and
are both differentiable, then
Before we begin, let us first discuss a WAF coordinate system. A WAF coordinate system contains an x-axis and two y-axes. The two y-axes are at right angles to each other, as seen in the illustration below.
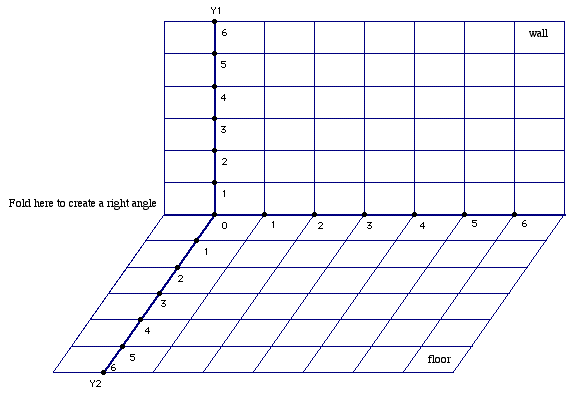
We will use the WAF coordinate system to geometrically explore the derivate of the product of two functions.
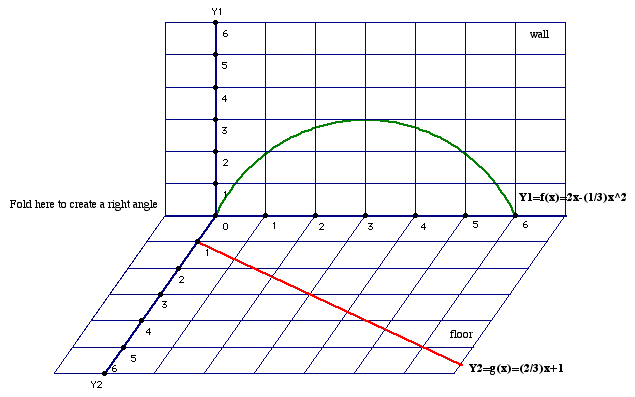
To begin, let's sketch the curves
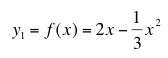on the "wall" and
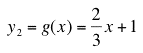on the "floor" of the
WAF coordinate system.
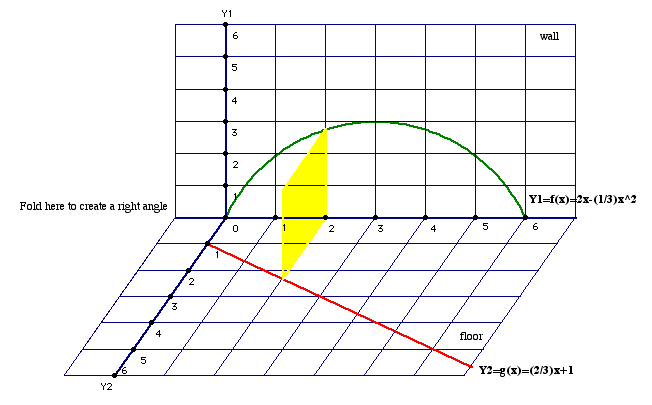
Next, cut out a rectangle with dimensions 
and
. Now, tape your rectangle to the
WAF coordinate system where it coincides with the function, as
seen in the illustration below where the yellow rectangle represents
your cut out rectangle.
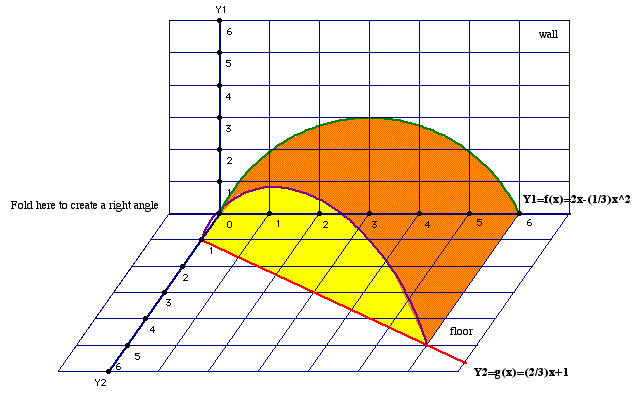
Now, cut out five more rectangles for 
and
for various values of x. It is recommended
that you create at least five more rectangles, for x having the
values 1, 3, 4, 5, and 6. By cutting out more and more rectangles,
you can begin to visualize the solid created if there were infinately
many rectangles, as seen in the illustration below.
Now, consider the function that defines, for any given x, the
area of the cross section. This cross section is also one of the
rectangles you previously cut out. Let's call this function 
. Then, 
.
Next, construct two more rectangles for some value of x and x+h as illustrated below. You need not tape your rectangles on your model, but consider where they would be placed.
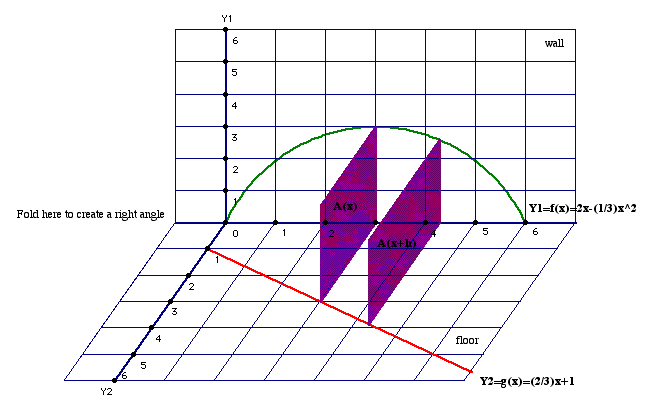
Now, how can we see geometrically what occurs to the function
when we take different values x
and x+h. Consider our rectangles just constructed.
Now, compute the lengths of the sides of each rectangle, A(x) and A(x+h).
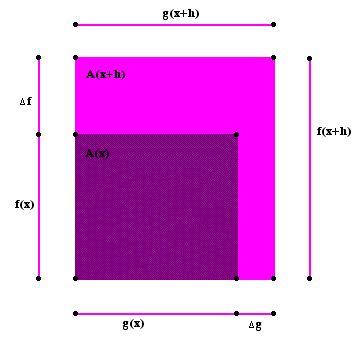
Now, can you determine what 
is?
Notice that 
. Now, find 
in terms of f and g. Do you get one of the
following?
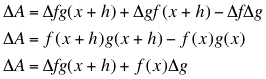
Now, assuming that the required limits exist and behave as we would expect, we can obtain the product rule from the last equation, as follows:
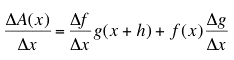
then follows 
. We have now derived
the Product Rule!
It may useful to check that we can use A(x) and A'(x) to compute values of f(x)g(x) and the derivative of f(x)g(x). As an example, let x =1/2, then the steps are as follows:
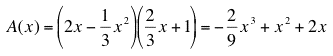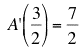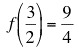and 
and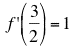
.
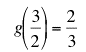and 
.
and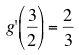 
.
.This task was adapted from ---- (1990) Derivative of a product: Exploration 2 of concepts of calculus for middle school teachers. Middle School Math Project. Salem, OR: The Math Learning Center.