

Consider the equation
Task: Explore the graphs in the xb plane.
Let us begin by considering the equation
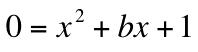
Now, to explore graphs in the xb plane, consider the following graph in which the above equation is in relation to the xb plane.
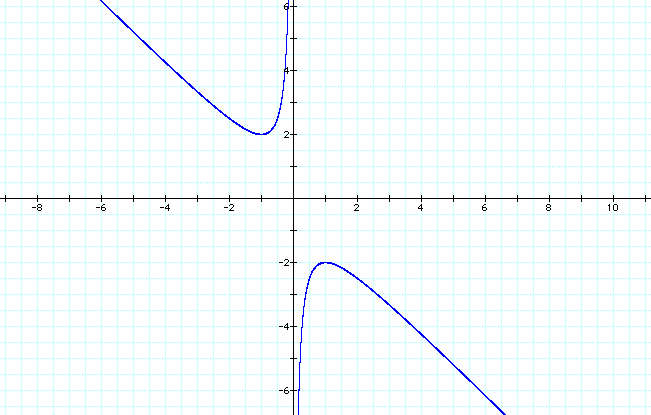
From the graph, notice the shape of the curve of the equation in the xb plane. What does this graph tell us about our equation?
Consider the graph when we include the line b=2.
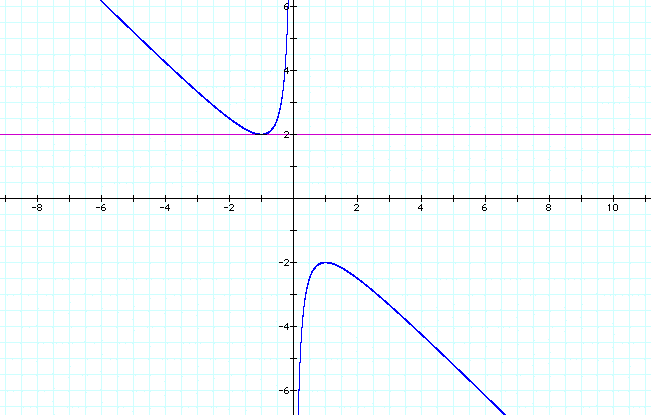
It can be seen from the graph that when we include the line b=2 that the line represents the real roots of our original quadratic equation. We can conclude that when b>2 or b=2 that we will have real roots. Additionally, when -2<b<2, we will have non real roots for our quadratic equation.
Using our above graph, let us consider instances when c is -1 versus 1.
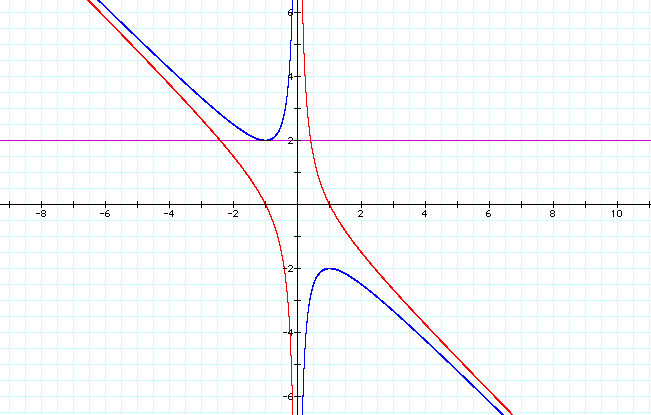
Similar to our graph when c=1, for c=-1 we are still able to see the roots of our quadratic equation. However, when c=-1, we can see that for any value of b we will have real roots.
Let us explore this further by examining our quadratic for various values of c. From our movie below we can see where are roots are for -10<c<10.
Now, isn't that something!