Five Quadratures of a Lune
In order to understand the five quadratures of a lune, we must first
understand the meaning of quadrature. The quadrature of any plane
figure means that there is a square which can be constructed that will
have the same area as the plane figure. To better understand this
concept lets look at the quadrature of a triangle.
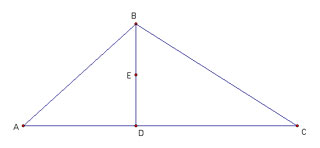
Let's begin with triangle ABC and construct its altitude BD, and it's
midpoint E.
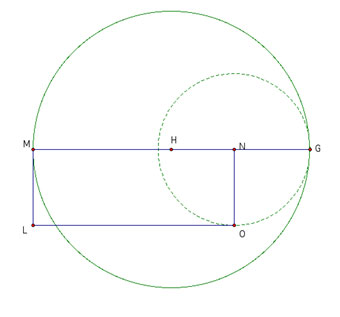
Now we construct rectangle LMNO with length BC and width DE.

Now we square the rectangle by extending MN to MG where NG is equal in
length to NO and H is the midpoint of MG and creating a circle with
radius MH.
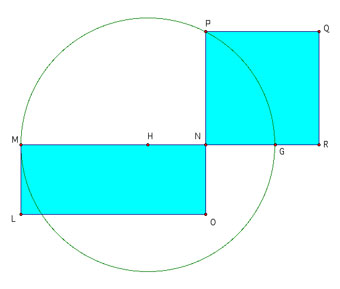
Now create segment NP which is perpendicular to segment MN and use this
segment as one side of the square NPQR. The area of the square
NPQR is equal to the area of the rectangle LMNO.
This quadrature can be proven using the pythagorean theorem and the
triangle HNP that is formed by the constructions.
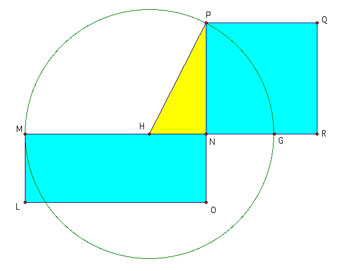
Looking at triangle HNP we have by the pythagorean theorem that (HP)2=((HN)2+(NP)2
which gives us that (PN)2=(HP)2-(HN)2=(HP-HN)(HP+HN).
So the area of the square NPQR is (HP-HN)(HP+HN). Now, we can see
that HP is the radius of the circle as are MH and HG, so we have that
MH=HG=HP. So we can say that MN=MH+HN=HP+HN and NO=NG=HP-HN by
our constructions. Now, we know that the area of rectangle LMNO
is (MN)(NO)=(HP+HN)(HP-HN) which is in fact the area of our
square. Therefore the areas of our square NPQR and our rectangle
LMNO are in fact equal.
Now we will look at the five quadratures of a lune, the region bounded
by two circular arcs with different radii.
Quadratures 1 & 2
Quadrature 3
Quadrature 4
Quadrature 5





