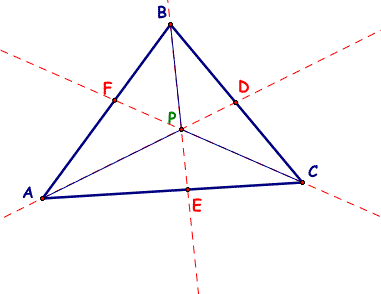
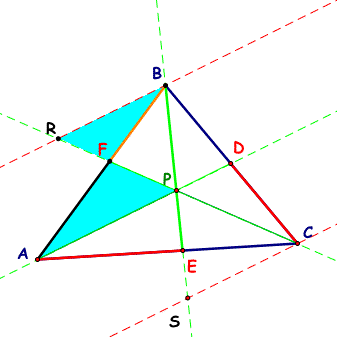
Create a triangle (ABC) and place point P arbitrarily inside of triangle ABC. Then by creating and extending lines I drew the following.
Explore the line segments AF, BD, and CE. Also explore the segments FB, DC, and EA. See below for a new picture with measurements included.
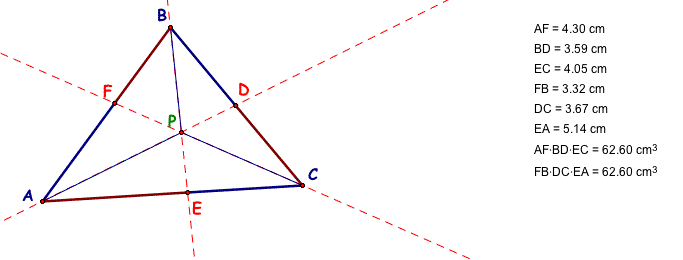
Note what happens when we calculate the 2 products of the 3 line segments as indicated: AF*BD*CE = FB*DC*EA = 62.60 cubic cm.
What if we chose a different location for point P?
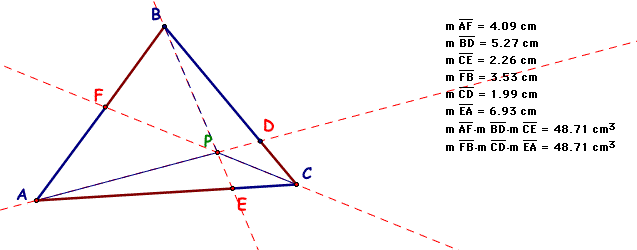
The products of the 2 sets of 3 line segments are still equal.
What if we looked at an obtuse triangle rather than acute with point P located inside this triangle?
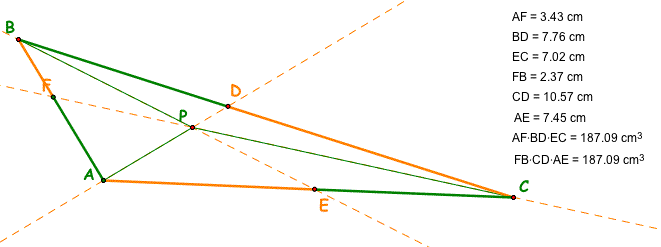
The products of the 2 sets of 3 line segments are still equal.
We have measured these line segments for 3 different triangles and found the products of the 2 sets of 3 line segments.
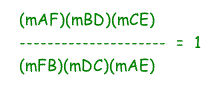is true.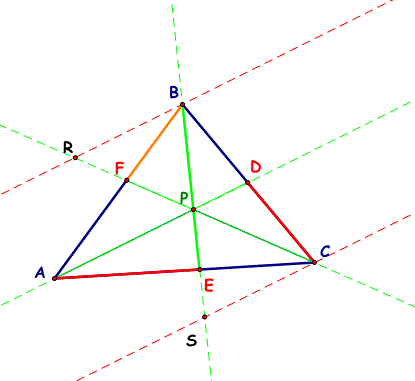
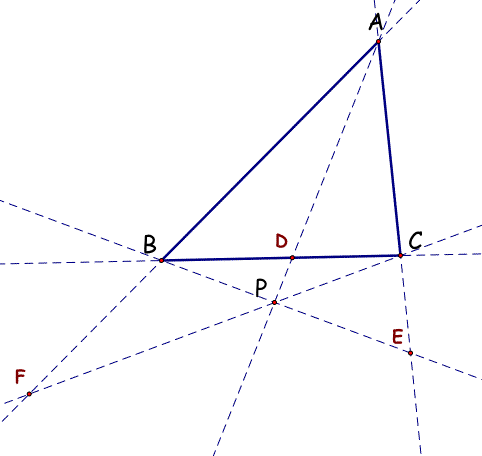
First, note that triangle BSC is similar to triangle BPD, angle CBS is congruent to angle DBP and angle BSC is congruent to angle BPD (similar angles, corresponding angles, & reflexive property).
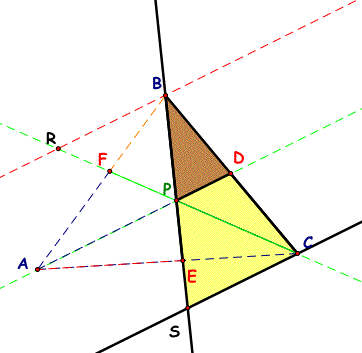
Thus,
BC/BD = SC/PD
because corresponding sides of similar triangles are proportional. Then, using cross multiplication
(BC)(PD) = (BD)(SC)
__________________
Second, note that triangle RCB is similar to triangle PCD, angles RCB and PCD are congruent, and angles BRC and DPC are also congruent (angle similarity, corresponding angles and the reflexive property).
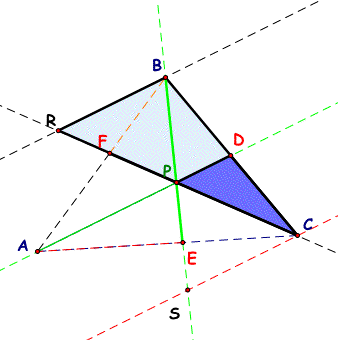
Thus,
BC/DC = RB/PD
because corresponding sides of similar triangles are proportional. Then, using cross multiplication
(BC)(PD) = (DC)(RB)
_______________
Thirdly, triangle FPA is similar to triangle FRB due to angle similarity. Angle AFP is congruent to angle BFR (vertical angles). Also, angle FAP is congruent ton angle FBR (alternate interior angles).
Thus,
AF/BF = AP/RB
because corresponding sides of similar triangles are proportional.
Then,
RB = [(BF)(AP)]/AF
_______________
Fourth, triangle ESC is similar to triangle EPA, angle CES is congruent to angle AEP, and angle SCE is congruent to angle PAE (angle similarity, vertical angles, and alternate interior angles).
Thus,
SC/AP = CE/AE
because corresponding sides of similar triangles are proportional.
Then,
SC
= [(AP)(CE)]/AE
_____________________
By using substitution with
(BC)(PD) = (BD)(SC) and (BC)(PD) = (DC)(RB)
we find the following is true:
(BD)(SC) = (DC)(RB)
and further substitution will give us:
(BD)[(AP)(CE)]/AE = (DC)[(BF)(AP)]/AF
_____________________
Finally, using cross multiplication we find the following to be true:
(BD)(AP)(CE)(AF) = (AE)(DC)(BF)(AP)
and we can remove (AP) because (AP)/(AP) = 1 and therefore,
(BD)(CE)(AF)/(AE)(DC)(BF) = 1
or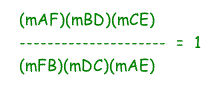
What if point P is outside or exterior to our triangle ABC? Click on the diagram below to open GSP then use your mouse to move point P around. Notice what happens to points D, E, & F as you manipulate the location of point P.
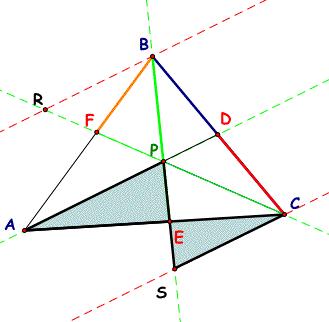
Show that when point P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4. When is this ratio equal to 4?
See the diagram below:
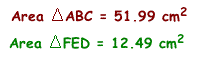
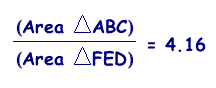
Click on the triangle above to open GSP. Then use your mouse to move P around inside the triangle. Watch how the ratio of the areas change as you move P. You may notice a time when this ratio is exactly equal to 4.
Where does point P have to be located in order for the ratio of the areas to be equal to 4? See below.
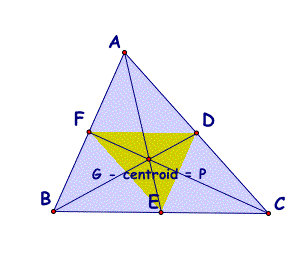
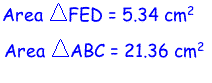
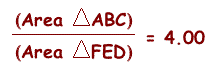
When point P is located on the Centroid (G) of triangle ABC, then the ratio of the area of triangle ABC to the area of triangle DEF is always equal to four.