I chose to explore Part 6 of Assignment 1 which included graphing and then exploring the equations : where n=2, 3, 4, 5, 24, & 25.

First ,I entered each equation into Graphing Calculator and generated a graph for the equation. See the equations and graphs below.

Once I began graphing these equations, I could somewhat predict what might happen as the exponent changed from an even number to an odd number.

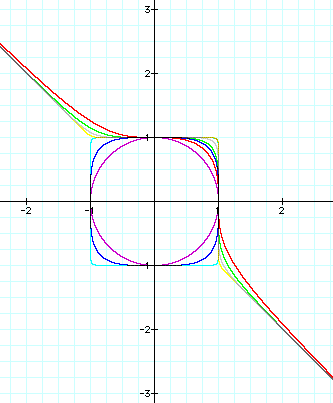
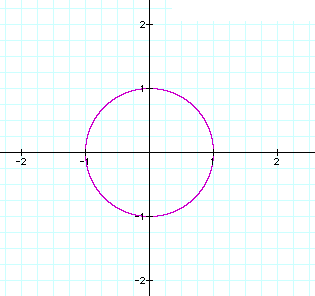
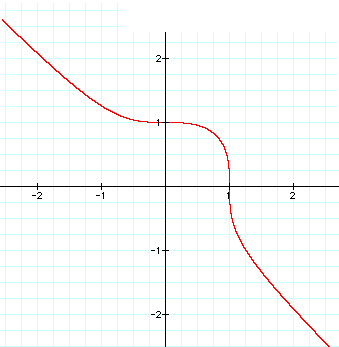
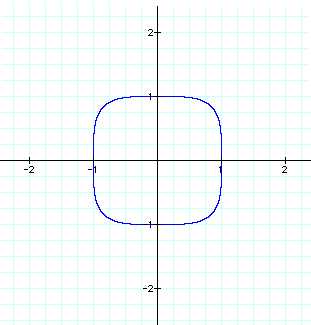
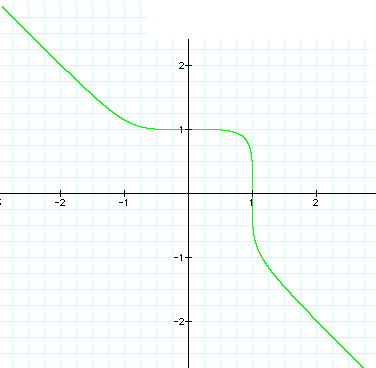
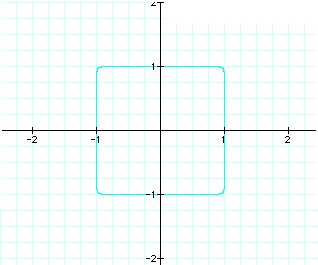
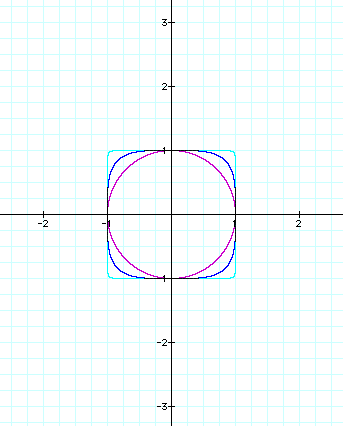
As illustrated in the graphs above, the equations with the even numbered exponents (2, 4, & 24) created the closed figures which center around the origin. While the graphs created by the equations with the odd numbered exponents (3,5, & 25) were not circular, rather , they were continuous. This prompted me to explore these equations and graphs further.

The three closed graphs generated by the equations with the even numbered coefficients all intersect the x and y axes at 1 and -1, thus the following 4 sets of (x,y) coordinate points are found on all three figures: (0,1), (1,0), (0,-1), and (-1,0). See the graph below.

This would make sense because when we plug in 2,4 or 24 in for n in this equation,

and set x equal to 0, then

 . Thus, when x = 0, for any even value of n, y = 1,or -1.

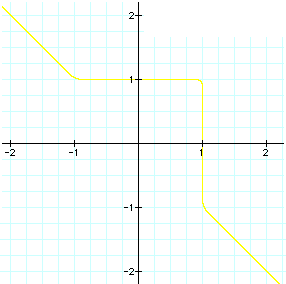
The 3 continuous graphs formed when n is an odd number (3, 5, or 25) in the equation

if x = 0, then

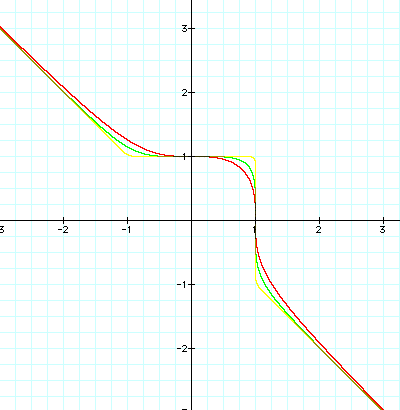
For any odd value of n, when x = 0, y has to be a positive 1.

Thus, every line generated by this equation while n is odd, passes through the coordinate points (0,1). Also, it appears that the lines created by this equation for different odd values of n always pass through the point (1,0). As you can see from the graph above, when x is negative, y is always positive. However, when x is positive and has a value between 0 & 1, y is also positive. But, when x is greater than 1, y becomes a negative value.

For example, look at this equationwhen x = 2 or x = -2. What will y equal in these 2 cases where n=3?

and y would be negative.

and y would be positive.

Return to Keri's Home Page