1. Investigate the equation
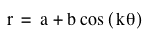for various values of 'k', where a = b and k is an integer.
2. Then compare with
for different values of 'k'.
3. Also, explore replacing .....cos() with sin()?
Investigation
of the graphs of the following equation when a = 1 = b and k is
an integer from 1,,7.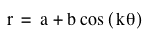
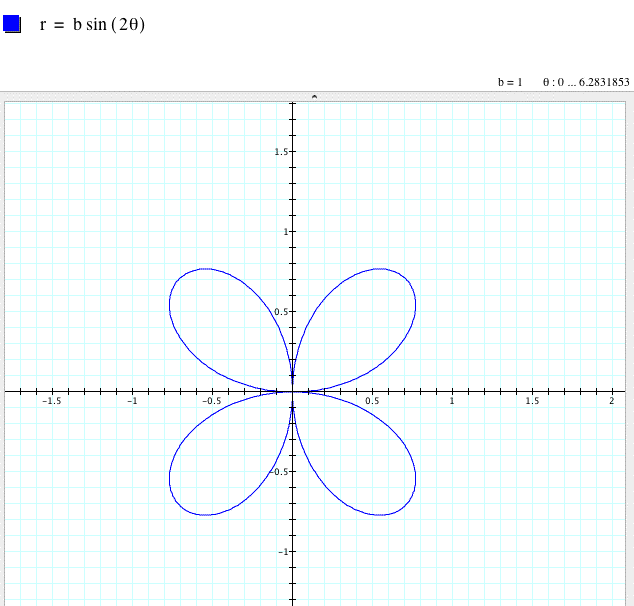
For k = 1,
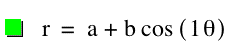
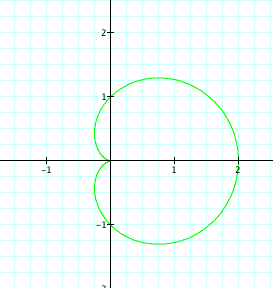
For k = 2,
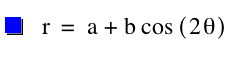
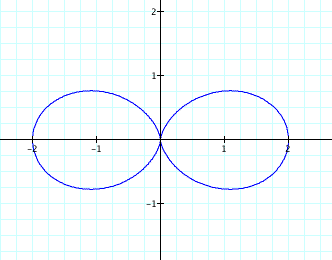
For k = 3,
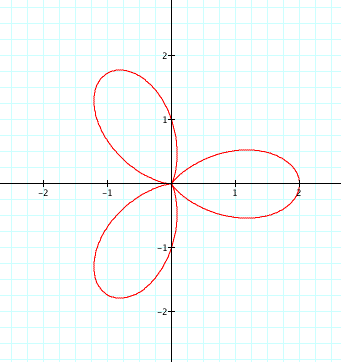
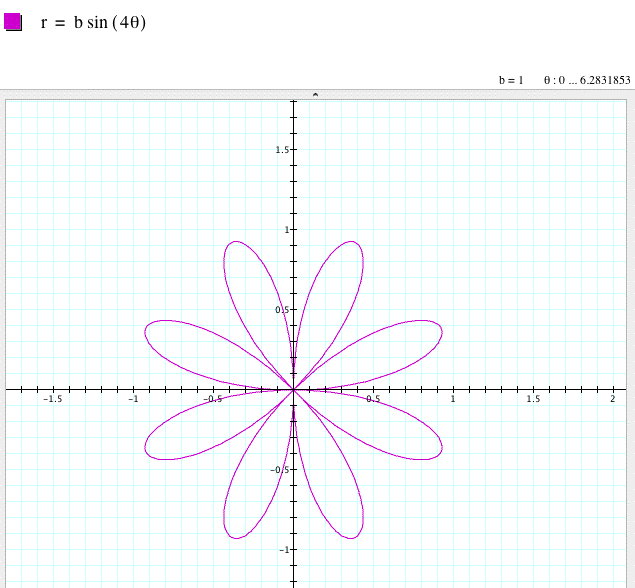
For k = 4,
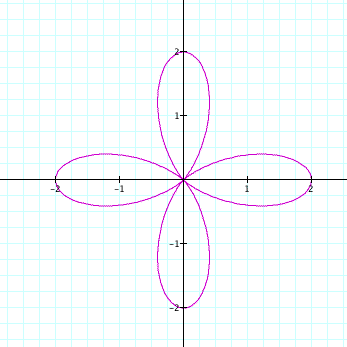
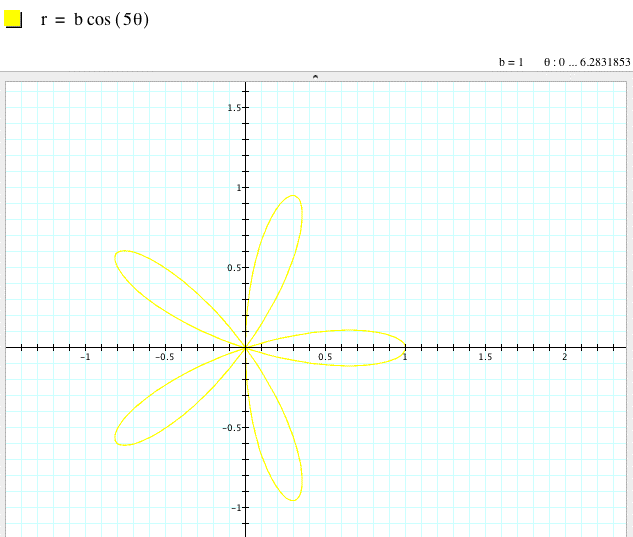
For k = 5,
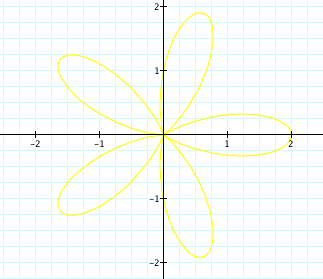
For k = 6,
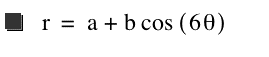
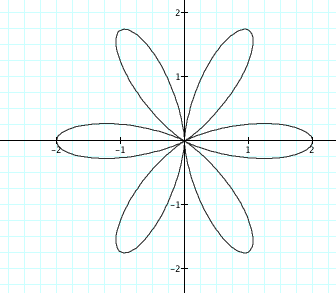
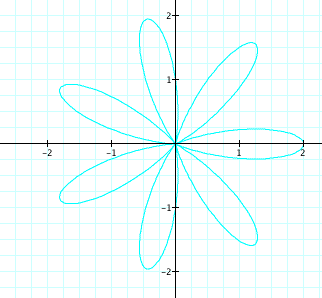
For k = 7,
Comparison
of and for three different
values of k.
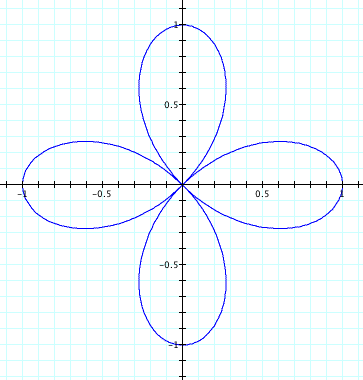
For k = 2,
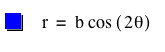
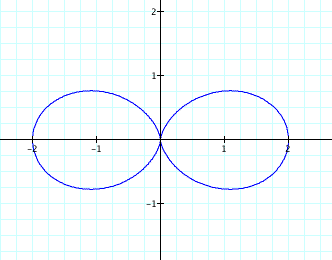
For k = 3,
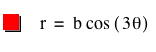
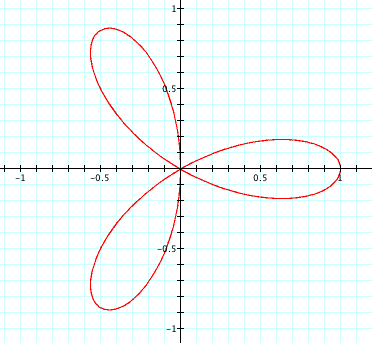
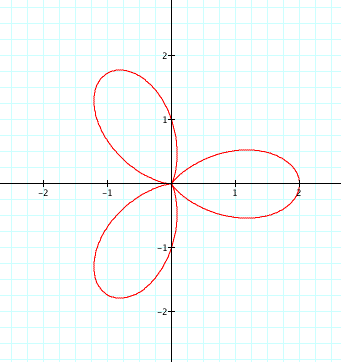
For k = 4,
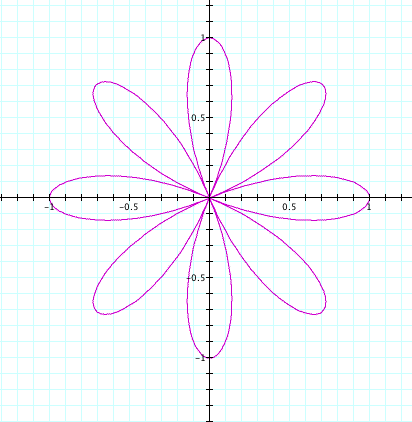
Notice that when k is an even integer (2 or 4 in this example), the number of leaves on the rose doubles when the a variable is omitted from our polar equation. On the other hand when k is odd (3 in this case), the number of leaves on the rose are equal.
Substituting
sin() for cos() in the equation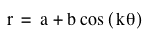
will change our graphs as follows (for k = 3, 4, 5, & 6):
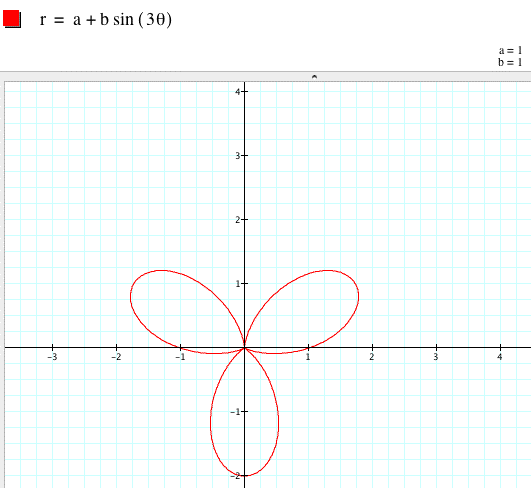
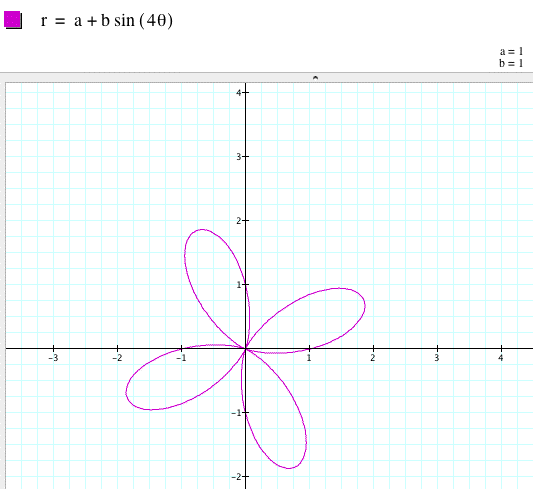
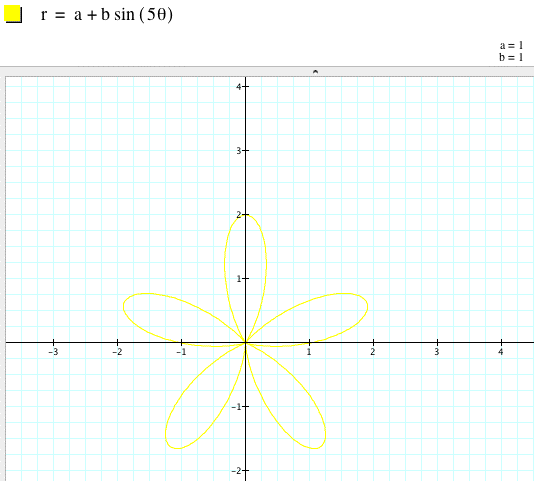
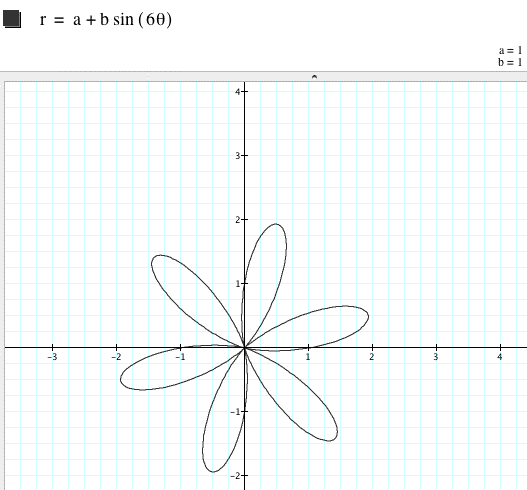
Substituting
sin() for cos() in the equation
will change our graphs as follows (for k = 2, 3, 4, & 5):
