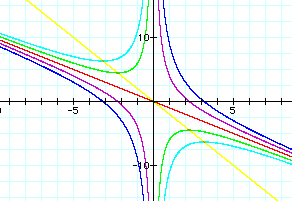
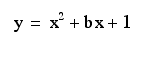where b = -3, -2, -1, 0, 1, 2, 3.Using Graphing Calculator to explore roots of quadratic equations. First I looked at the graphs for the following equation
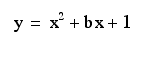where b = -3, -2, -1, 0, 1, 2, 3.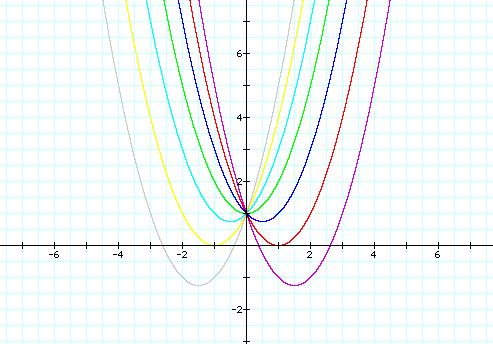
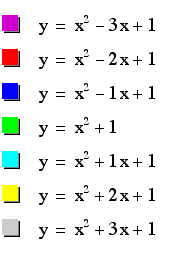
Note that all of these functions intersect, or pass through, the point (0,1). This is the point where b=0. When b is negative (-3, -2, or -1), the vertex of the parabola falls to the right of the y-axis. When b is positive (1, 2, or 3), the vertex of the parabola is located to the left of the y-axis. It might be helpful to see how this function moves along the xy-axis while b changes values.
to see an animation of 
where
b = -3, -2, -1, 0, 1, 2, & 3.
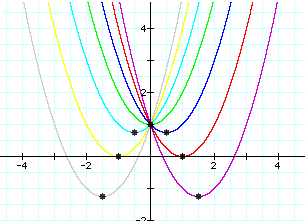
In order to find the graph of the equation that intersects all seven of these points (locus of vertices), we first note that all of our graphs pass through the point (0,1). Also, the roots of this new concave down parabola are 1 & -1. See new graph below.
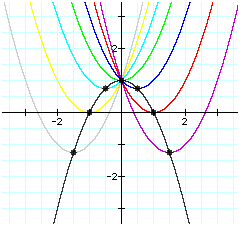
We can see that y = 0 when x = 1 or -1 (the roots of our equation). Thus
or
which creates a concave up parabola. Our parabola is concave down thus the equation for the locus of the vertices of parabolas is:
Examining the xb plane.
Consider the equation
Graphing this equation in the xb plane will give us the following:
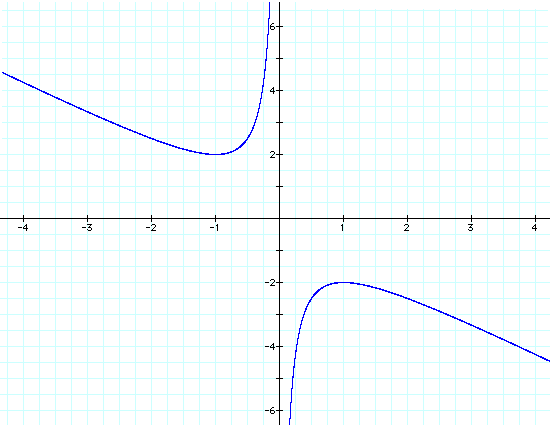
Now if we choose any value for b and overlay this line onto the previous graph shown in the xb plane,the new graph would look as follows:
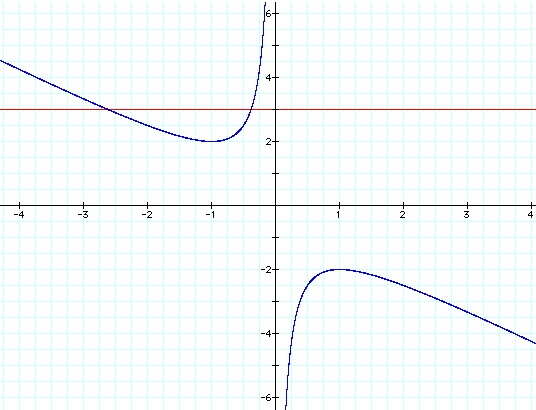
I chose to set b = 3. Thus,
the red line displayed in the graph above is parallel to the x-axis
and is the line represented when b = 3. As you can see, this line
intersects one of our curves created by the equation.
These 2 points of intersection correspond to the roots of the
original equation for that value of b. Let's look at the graph
again and add the line where b = 2.
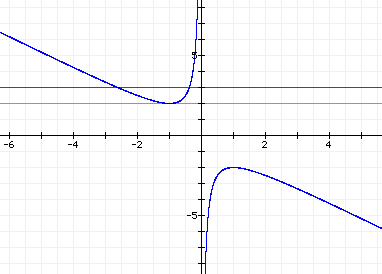
By examining these curves and lines, note that when b = 2, we only have one negative root (or one point where our original function of x is equal to 0). In this case it happens to be the point of tangency to the x-axis. When b > 2, there are 2 negative roots to our equation. Also, when b = -2, we have only one positive root and when b < -2 there are 2 positive roots. On the other hand, when -2 < b < 2 there are no roots to our equation.
What if c = -1 instead of +1?
Thus, we would have the equation
and the following graph.
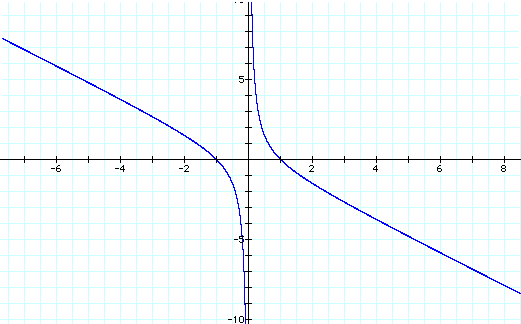
In this case, any chosen value for b would give us two roots to our original equation.
What if we look at several different values for c?
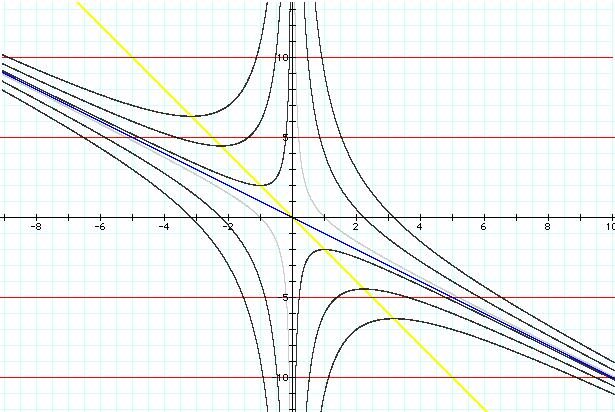
Take a look at the graph below which is an overlay of the graphs of our original equation on the xb plane with c = -10, -1, 0, 5, & 10.
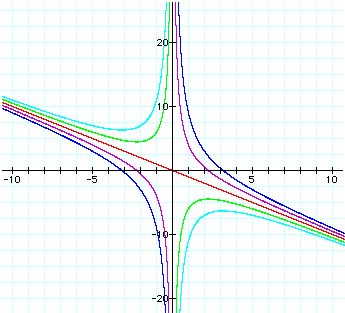
Adding the graph of the line: 2x + b = 0 (the yellow line that passes through the origin)
If we were to overlay the graphs of the lines formed by b = 5, b = 10, b = -5, and b = -10 , our new graph would show that the yellow line formed by the equation, 2x + y = 0, actually bisects the parabolas at the midpoints between their respective roots. See below.
For example, when b = 3 we can look at the parabola formed by
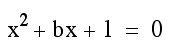
and plot a point where our yellow line intersects this parabola - it is the midpoint. See below. The yellow line is the equation, 2x + b = 0, and the black line is the equation, b = 3. As we found out earlier in our exploration in the xb plane, there are 2 roots to our original equation when b = 3. Our parabola intersects b in 2 places. The red point formed by the intersection of b = 3 & 2x + b = 0 happens to be the midpoint of the two roots (intersections on the parabola).
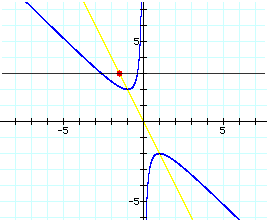
The coordinates for this red point of intersection are (-1.5, 3). The x-coordinate of -1.5 can also be found by looking at the quadratic formula, specifically the portion ( -b/2a ). In this case it would be -3/2. See the quadratic formula, used to find the roots of a quadratic equation, below.
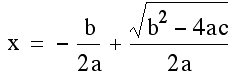or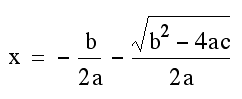 
If were to plug in our values for a, b, and c (1, 3, & 1 respectively), we would get the following:
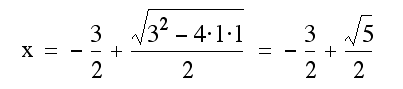and
.
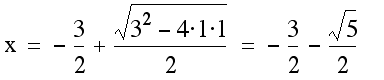Thus the two roots of our original equation when b=3 (y=3), would be equal to