
I. Centroid
The Centroid of a triangle is defined as the common intersection of the three medians of a triangle, where a median of a triangle is the segment from the vertex to the midpoint of the opposite side. See the triangle ABC below.

II. Orthocenter
The Orthocenter of a triangle is found at the common intersection of the three altitude lines of a the triangle. See the triangle DEF below.

III. Circumcenter
The Circumcenter of a triangle is the point in the plane equidistant from the three vertices of the triangle. In order to find the Circumcenter of a triangle, first find the three medians of the triangle and then use these median points to find the perpendicular bisectors of each side of the triangle. The intersection of the three perpendicular bisectors will be the Circumcenter. See the triangle XYZ below.

The Circumcenter of a triangle is the center of the circumscribed circle of that triangle. See the triangle XYZ again below, displaying the Circumcenter, C, and the circumscribed circle.

IV. Incenter
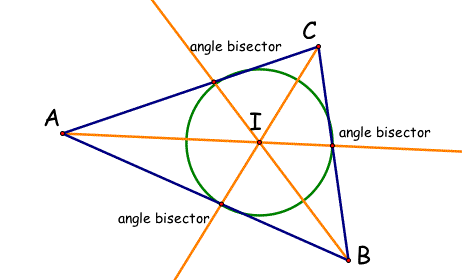
The Incenter of a triangle is the point on the interior of the triangle that is equidistant from the three sides. It can be found by bisecting all three of the angles within a triangle. The point of intersection of the three angle bisectors is called the Incenter. The Incenter is also the center of the inscribed circle of the triangle. See the triangle ABC below showing the 3 angle bisectors in orange and the Incenter, I. Also, the inscribed circle is shown in green.

A medial triangle is formed by connecting the three midpoints of a the three sides of any triangle. See picture below. The smaller shaded region is the medial triangle for the triangle ABC.

In order to compare the 4 centers of triangle ABC to the 4 centers of ABC's medial triangle, first I found the centers of the original triangle ABC which are labeled as follows:
Centroid is labeled G1,
Orthocenter is labeled H1,
Circumcenter is labeled C1,
and the Incenter is labeled I1.

Then I used GSP to find the same 4 centers of the medial triangle. The figure below has the medial triangle's centers labeled in blue lower-case letters as follows: g2 = Centroid, h2 = Orthocenter, c2 = Circumcenter, and i2 = Incenter.
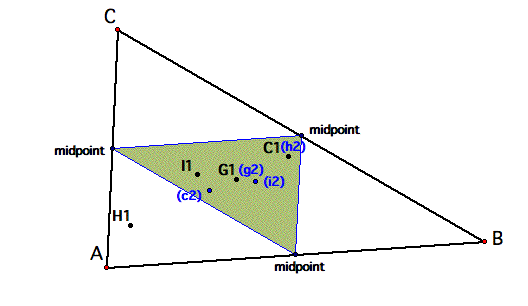
Note that the Centroid of the original triangle ABC, labeled G1, is the same point as the Centroid of the medial triangle, g2. Also note that the Circumcenter of the triangle ABC, labeled C1, is the same point as the Orthocenter of the medial triangle, h2.