THE QUESTION?
If you have an equilateral triangle and create a new triangle of the medians - will the new median triangle be equilateral also?
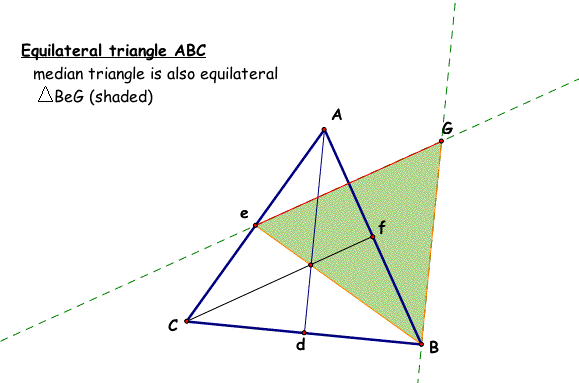
Look at the figure below created using GSP. The original triangle is ABC and the three medians are Cf, Ad, and Be. I chose to use the median Be for the base of the new median triangle. Then, in order to finish constructing this new median triangle, I used GSP's parallel line construction tool . This tool created the 2 lines eG and BG and as you can see these two lines intersect at point G - and the new median triangle is formed (shaded in green). Because ABC is an equilateral triangle, the 3 medians are also equilateral and equal to the three sides as well. Thus the new median triangle is an equilateral triangle just as the original.

THE QUESTION?
If you have an isoceles triangle and create a new triangle of the medians - will the new median triangle be isoceles also?
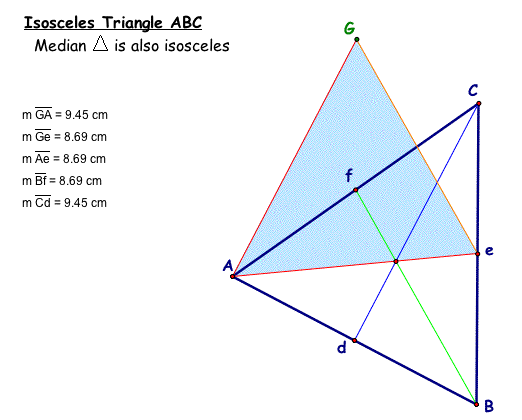
Using GSP, I drew the isoceles triangle ABC (using the perpendicular line tool to create an altitude for the triangle). The three medians are Ae, Cd, and Bf. Again I selected a base, Ae, for the median triangle. Then I used the parallel line tool in GSP to create the other 2 sides of the new median triangle, AG & Ge. As shown in the diagram below, the new triangle AGe is also an isoceles triangle (shaded in blue) - notice the measurements of the line segments' lengths.
THE QUESTION?
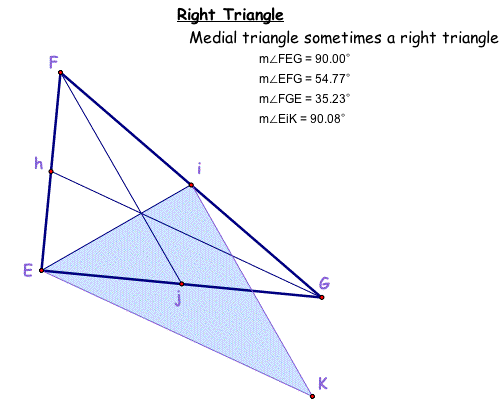
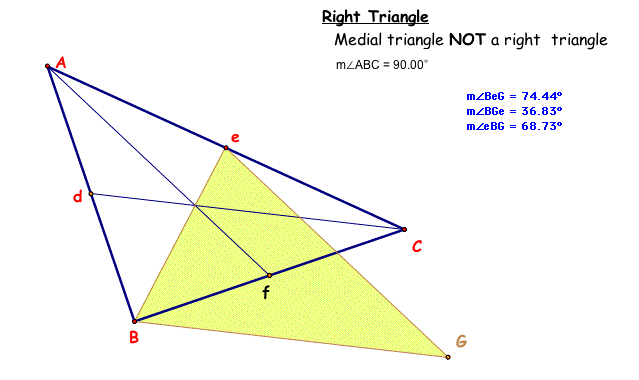
If you have an right triangle and create a new triangle of the medians - will the new median triangle be a right triangle also? If so, in what instances will the median triangle also be a right triangle?
-----------------------------------------------------------------------------------------
When is the median triangle a right triangle? As you can see in the diagram below, when the original right triangles' measure 90, 55, and 35 degrees, the median triangle formed will be a right triangle.