Exploring Pedal Triangles for various locations of Pedal Point P:
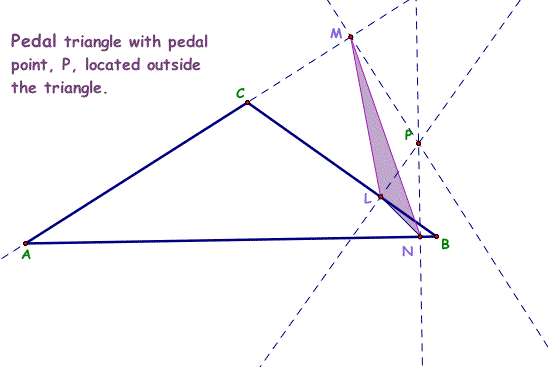
1. Construct any triangle ABC and point P anywhere on the same plane. The diagram below shows the construction of a pedal triangle, LMN, when the pedal point, P, is located on the outside or exterior of the triangle. The pedal triangle is shaded purple.
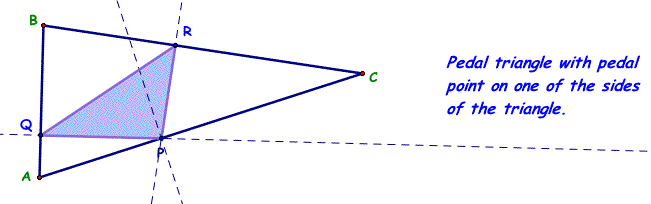
2. Pedal triangle, PQR, was constructed for triangle ABC and the pedal point, P, located on one of the sides of the triangle (side AC).
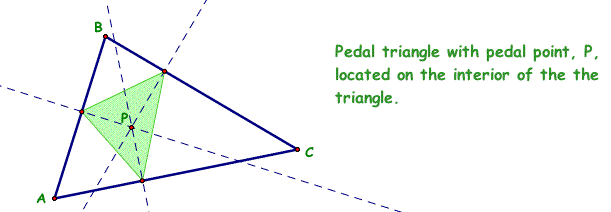
3. Pedal triangle of ABC with pedal point, P, located on the interior of the triangle.
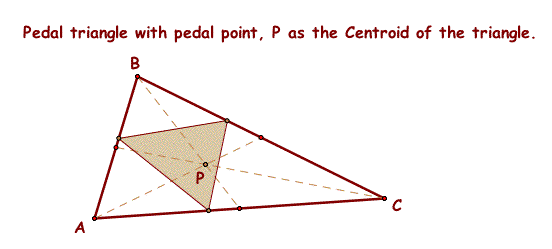
4. Pedal triangle of triangle ABC with the Pedal point, P, being the Centroid of triangle ABC.
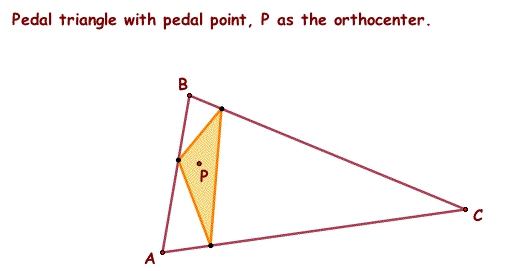
5. Pedal triangle of ABC with Pedal point, P, as the orthocenter of triangle ABC.
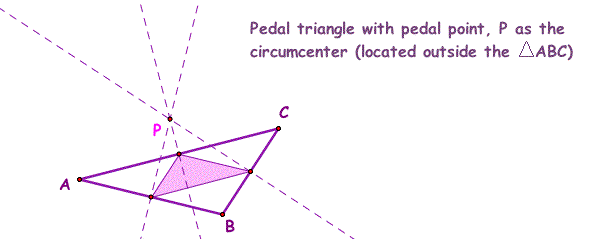
6. Pedal triangle of ABC with the Pedal point, P, as the Circumcenter of triangle ABC (P located on the exterior of triangle ABC).
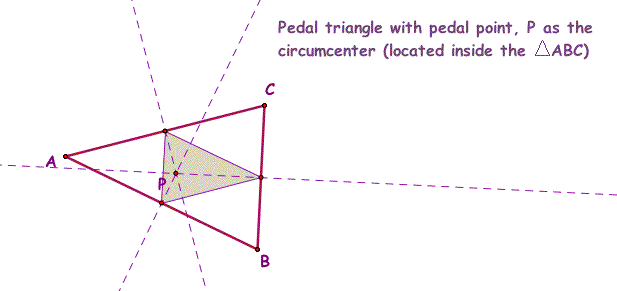
7. Pedal triangle of ABC with Pedal point, P, as the Circumcenter of triangle ABC (P located inside triangle ABC).
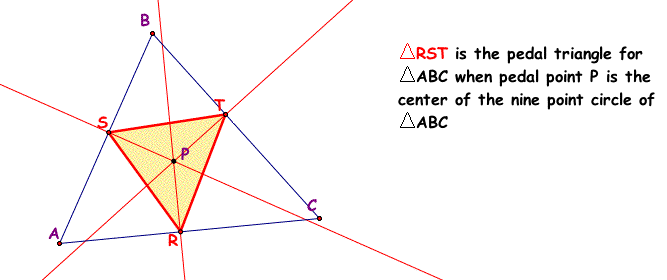
8. Pedal triangle, RST, of triangle ABC where the Pedal point, P, is the center of the nine point circle of triangle ABC.
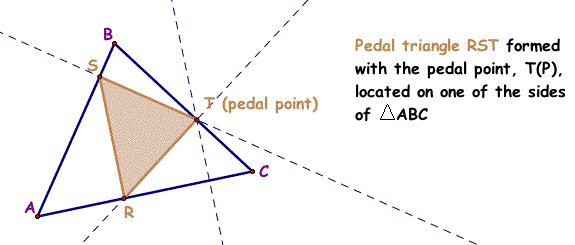
9. Pedal triangle, RST, of triangle ABC, where the Pedal point, P(T), is located on one of the sides of triangle ABC (side BC).
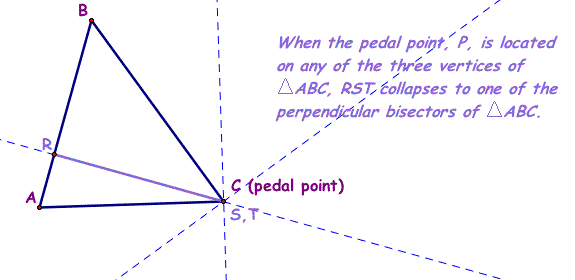
10. When the Pedal Point (C) is located on any of the three vertices of a triangle (anywhere on the circumcircle of triangle ABC), the Pedal triangle, RST, collapses to one of the perpendicular bisectors of triangle ABC. The three vertices of the Pedal triangle become collinear - we have no triangle.
11. The Simson line is the line segment created when the three vertices of the Pedal triangle are collinear. See the green line in the diagram below.
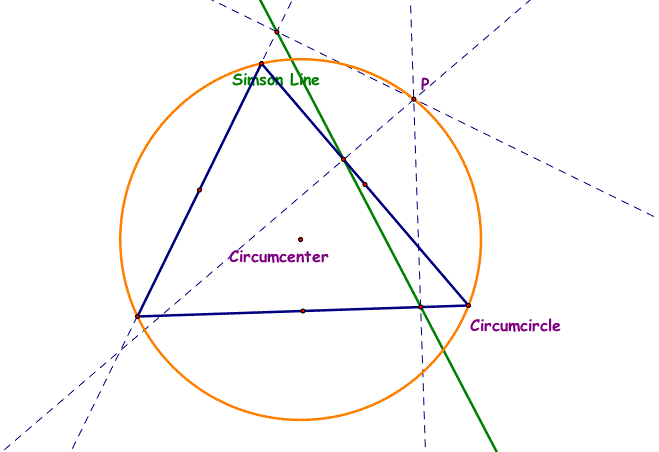
See the Simson line animated as point P travels counter-clockwise around the circumcircle. Just click on the diagram below which will open a GSP file. Then click on the Animate Point P button and observe.