![]()
A parametric curve in the plane is a pair of functions
![]()
where the two continuous functions define ordered pairs
(x,y). The two equations are usually called the parametric equations of a
curve. The extent of the curve will depend on the range of t and your
work with parametric equations should pay close attention the range of t
. In many applications, we think of x and y "varying with time
t " or the angle of rotation that some line makes from an initial location.
Explorations
Graph :
![]()
How would the graph change for various a and b where 0 ≤ t ≤ 2π?
Up above a and b equaled one. Will the graph change if a and b were still equal however neither equaled one? Let's try it.
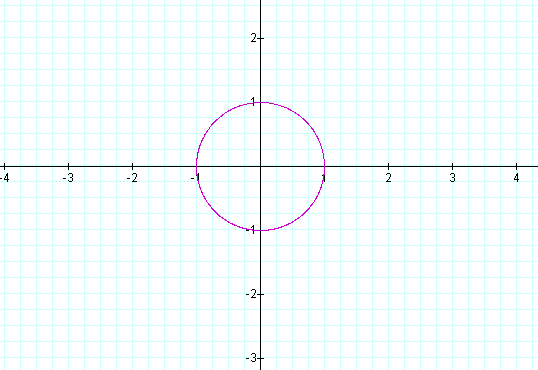
Graph: x = cos (at) and y = sin (bt) for a = b = 2 and a = b = -1.
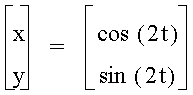
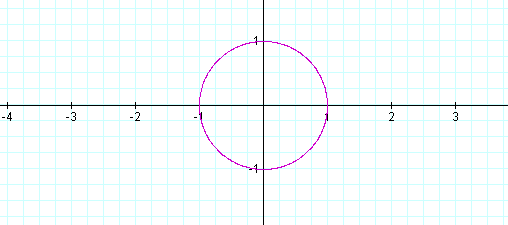
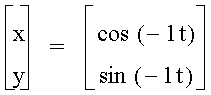
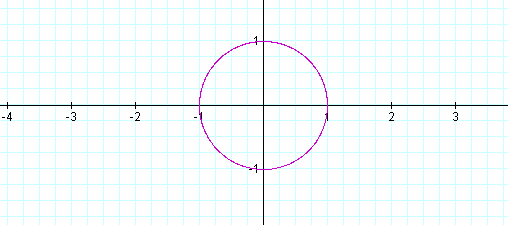
As you can see as long as a and b are equal the graph looks the same as our 1st graph. What about when a>b?
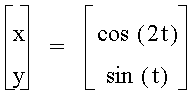
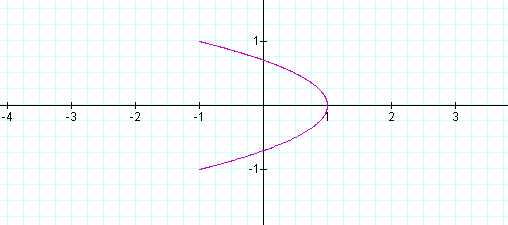
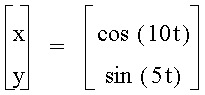
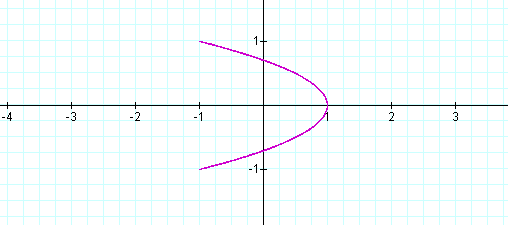
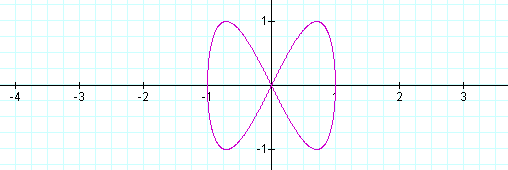
I noticed when b is 1/2 of a , a sideways parabola occurs! Let's explore some more.
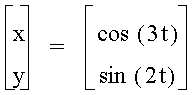
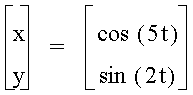
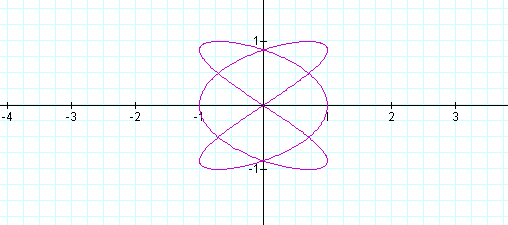
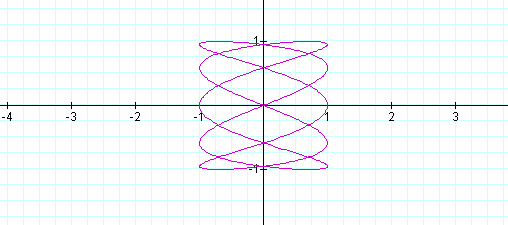
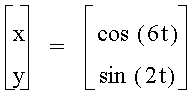
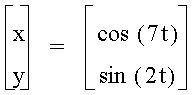
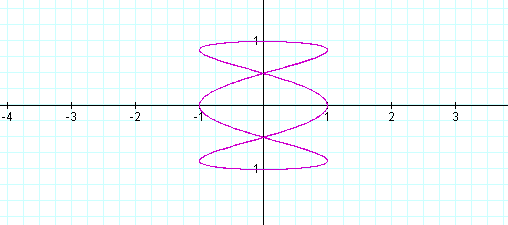
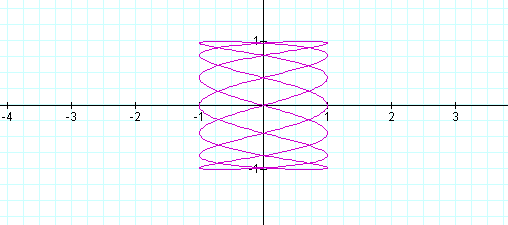
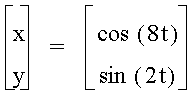
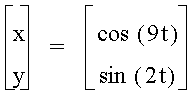
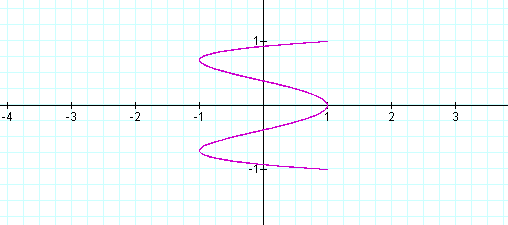
As you can see, some interesting shapes are occurring. Let's see what happens when a<b.
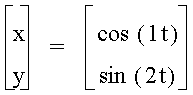
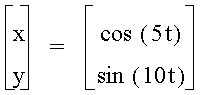
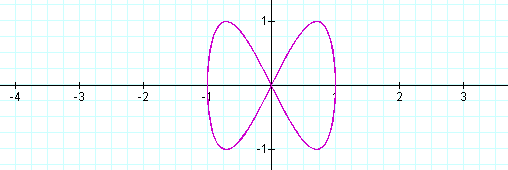
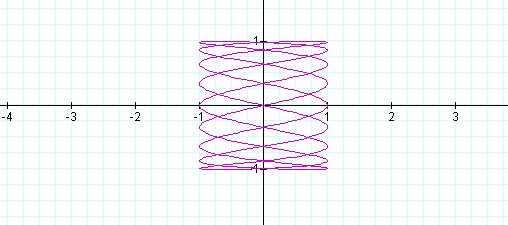
When a is 1/2 of b the same shape occurs again, however, it is different than when b is 1/2 of a. Let's explore some more.
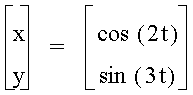
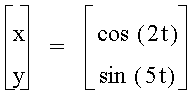
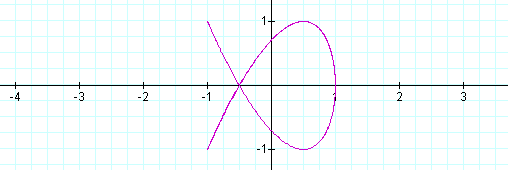
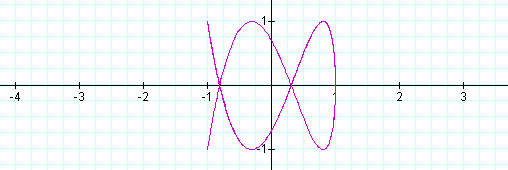
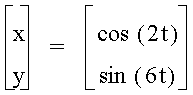
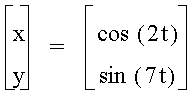
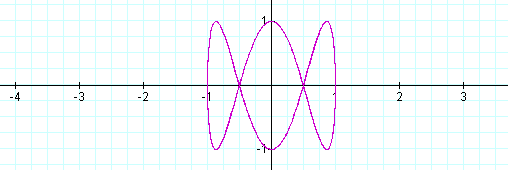
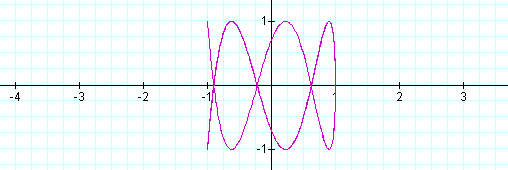
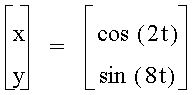
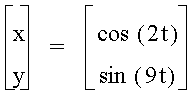
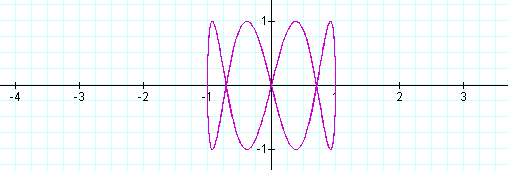
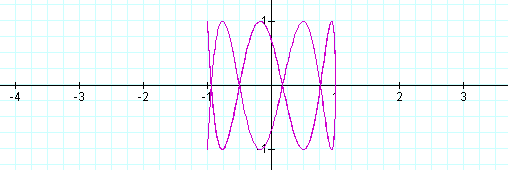
When a<b, the odd numbers take on a slightly different shape than the even. The number of loops in the graph increases as the b increases as well. The graph is also more horizontal now, where as, when a >b, the graphs were more vertical.