Investigate
When a, b and k equals 1, the graph looks like this:
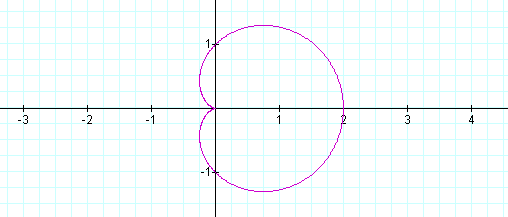
Let's keep a and b equal to one and vary k. When k = 2 the graph looks like this:
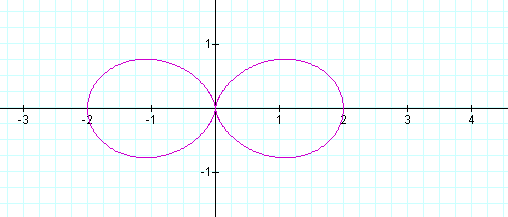
We get two leaves. Let's try k = 3, 4 and then 5.
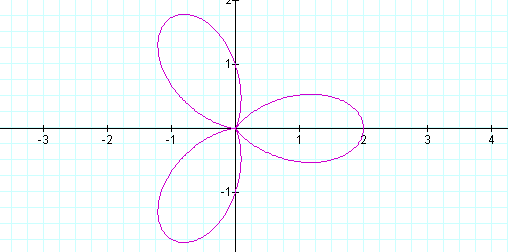
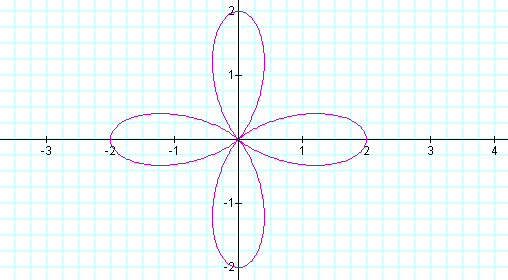
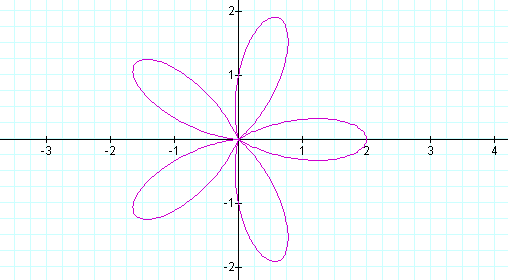
It seems as k increases the number of leaves increases. In fact, the number of leaves equals k.
Compare with
![]()
When b and k equals 1, the graph looks like this:
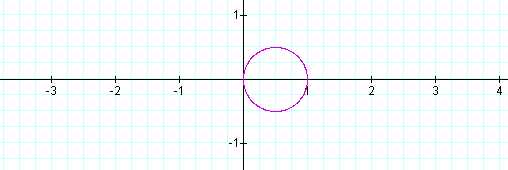
Now the graph looks like a circle. Let's see what happens when we change k to 2.
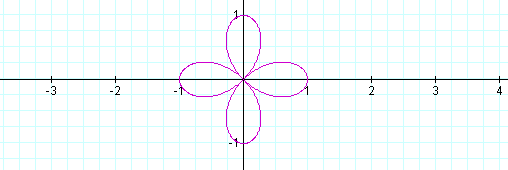
Four leaves! Let's look at the graph when k = 3, 4, and 5, respectively.
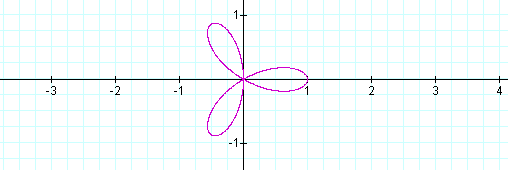
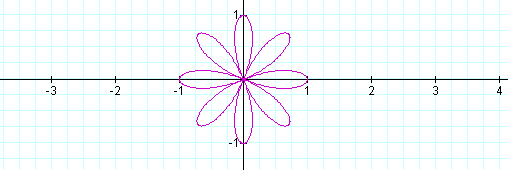
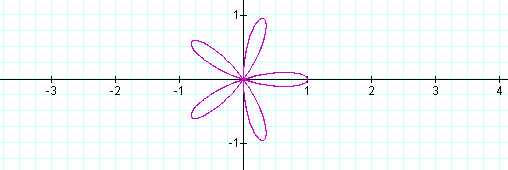
It looks as if the number of leaves equals k when is is odd, but doubles k when it is even.
What if . . . cos ( ) is replaced with sin( )?
When a, b and k equals 1, the graph looks like this:
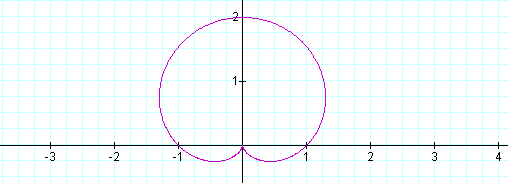
It rotated! Let's keep a and b equal to one and vary k. When k = 2 the graph looks like this:
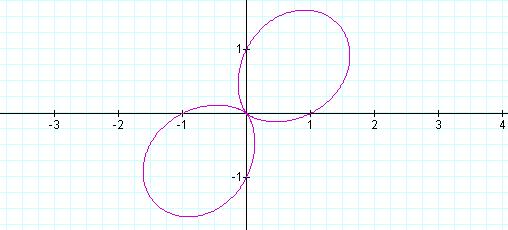
Same graph as cos, but rotated again! Let's try k = 3, 4 and then 5.
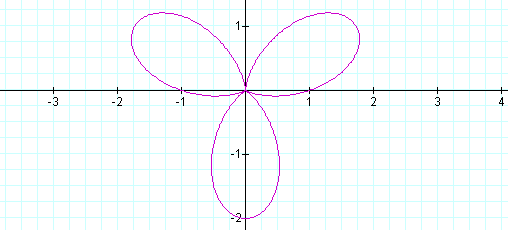
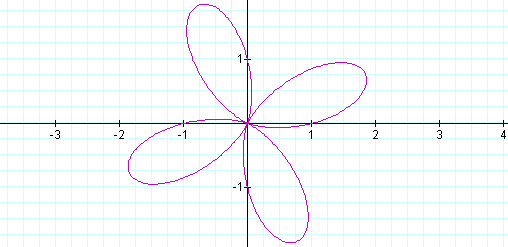
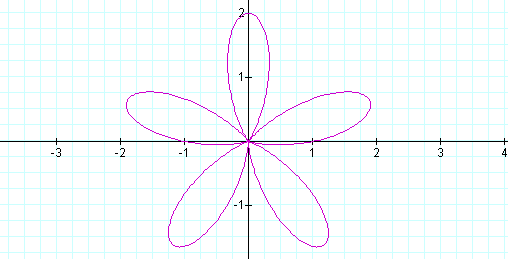
Again, all the same graphs as cos, but rotated. Let's compare with b sin (k0).
When b and k equals 1, the graph looks like this:
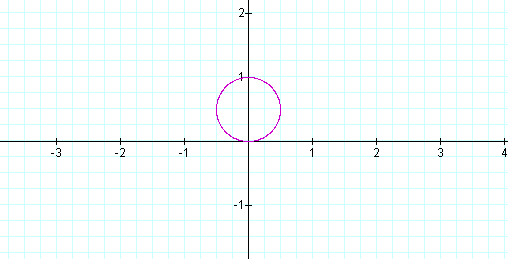
Let's see what happens when we change k to 2.
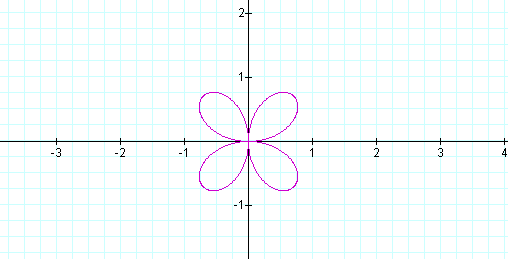
Let's look at the graph when k = 3, 4, and 5, respectively.
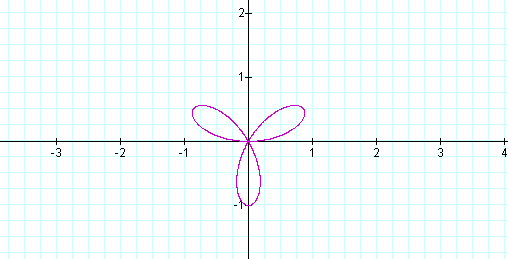
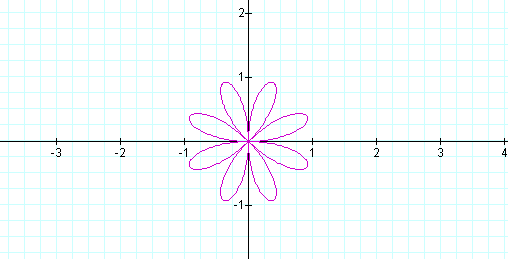
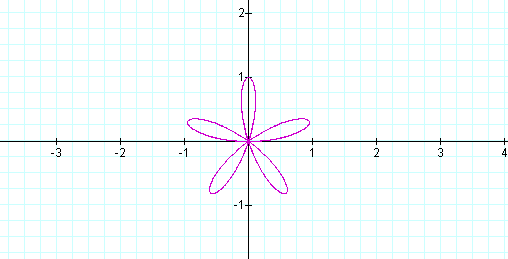
Just as I suspected, the same graphs as above, but, rotated!