Problem 7:
Explore different graphs of y = ax^2 on the same axis using different values of a.
First, let's look at the graphs separately. Consider, y = x^2. (a = 1)
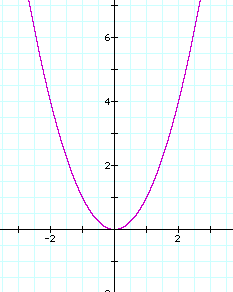
Now, let a = 2.
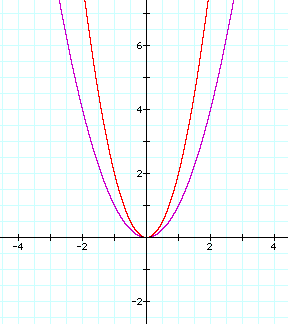
When the coefficient a was changed from 1 to 2 the graph became narrower. Is it safe to assume the bigger a gets the narrower the graph of y=ax^2 will become? Let's try a=5 and a=100.
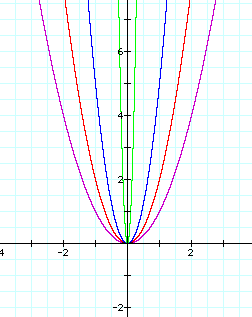
Yes. It seems as a gets larger, the graph of y=ax^2 gets narrower.
How will y=a^2 behave when a < 1, but >0? Let a = 1/2
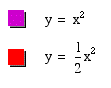
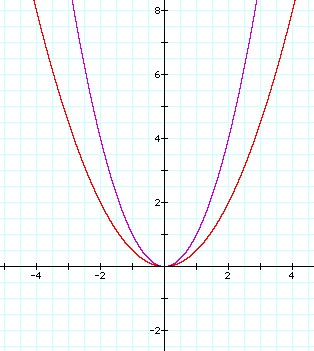
Now the graph of y=ax^2 is getting wider! Let's try some smaller values and see what happens. Let a = 1/5 and a=1/100.
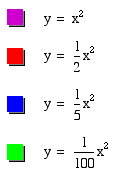
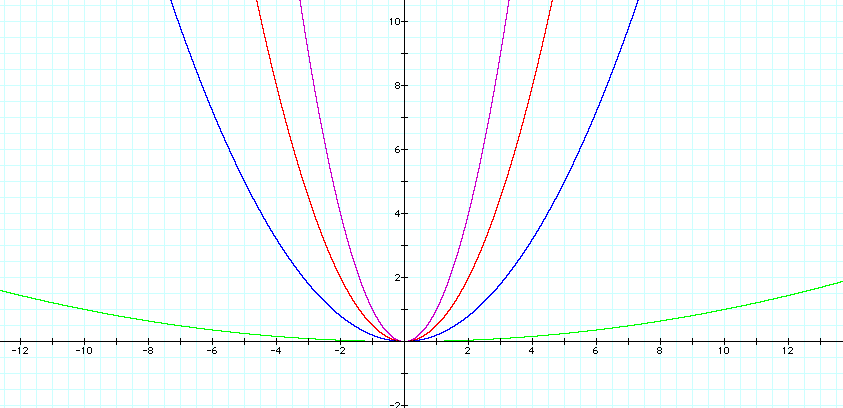
As a gets smaller, the graph of y=ax^2 is definitely getting wider.
What happens when a=0?
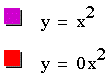
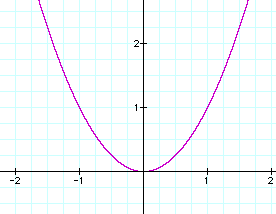
When a=0, the function y=ax^2 is not a quadratic equation anymore. Therefore, a parabola is not drawn. When a=0, the function become a point (0,0)
What happens when a is negative?
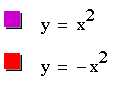
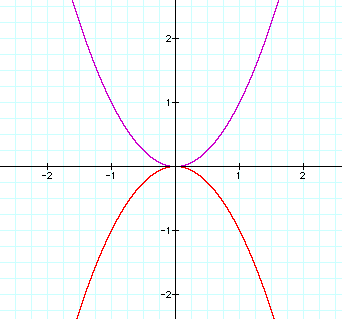
The graph of y=-x^2, is a reflection of y=x^2. Does the negative sign flip the parabola when a is between 0 and -1?
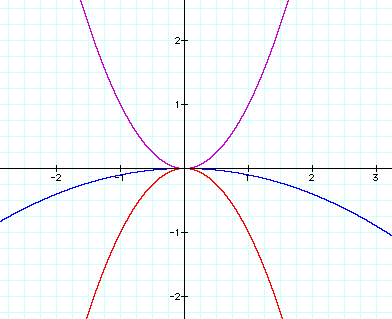
The graph is flipped and is wider than the graph of when a=-1.
Let's look at a graph when a < -1. Let a = -5.
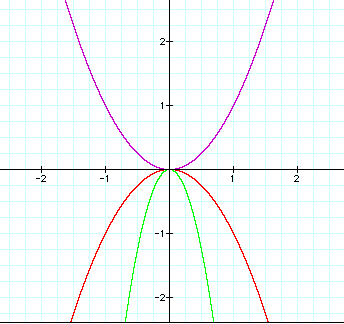
When a<-1, the graph becomes narrower than y=-x^2.
In conclusion, when the graph of y = ax^2 was explored with different values of a, we found the following:
Using a =1 as the parent function (comparing the graphs to y=x^2),we know:
1. a<1, but >0 the graph becomes wider.
2. a>1, the graph becomes narrower
3. a=0, the parabola does not exist
4. a<0 but > -1, flips and wider
5. a<-1, flips and narrower
6. a = -1, reflection of y=x^2