By the end of this write up, my geometry students should know the definition of and how to construct a centroid, orthocenter, circumcenter and incenter. Why are they called the centers of a triangle?
The Centroid
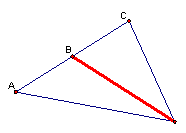
A median of a triangle is a line segment that joins a vertex of a triangle and the midpoint of the opposite side. See the diagram below:
The red line is the median because it is a line segment that joins a vertex of the triangle to the midpoint of the opposite side. Line segment AB is congruent to line segment BC.

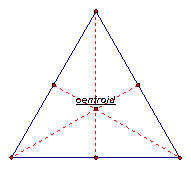
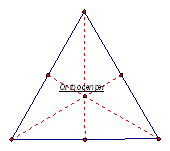
Since there are 3 vertices in a triangle, there must be three medians. One coming from each vertex. A centroid is the common intersection of the three medians of the triangle. See the diagram below of the centroid of an acute, obtuse, right, and equiangular triangle.
Acute
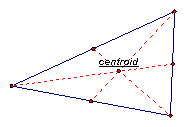
Obtuse
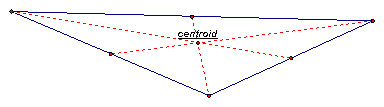
Right
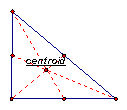
Equiangular
The Orthocenter
An altitude has one endpoint at a vertex of a triangle and the other on the line that contains the side opposite that vertex so that the segment is perpendicular to this line. See the altitude below:
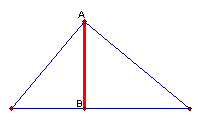
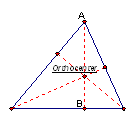
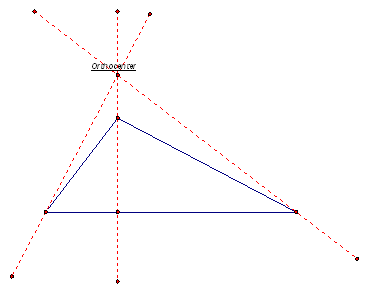
Line segment AB is an altitude. The orthocenter of a triangle is the common intersection of the three lines containing the altitudes. An altitude does not always have to be inside a triangle. Therefore, an orthocenter is not always inside a triangle. Look at the orthocenters below in the different types of triangles:
Acute
Obtuse
Right
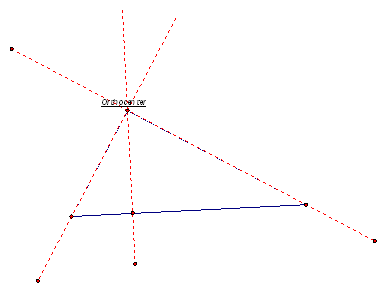
Equiangular
The Circumcenter
A perpendicular bisector is a line or line segment that passes through the midpoint of a side of a triangle and is perpendicular to that side. Since it has to be perpendicular, it too like the altitude does not have to be located inside the triangle. See a perpendicular bisector below:
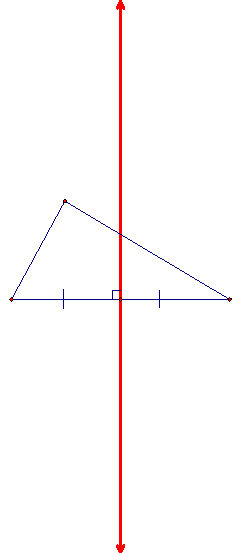
The circumcenter of a triangle is the point in the plane equidistant from the three vertices of the triangle. Since a point equidistant from two points lies on the perpendicular bisector of the segment determined by the two points, the circumcenter is on the perpendicular bisector of each side of the triangle and does not have to be located inside the triangle. See the circumcenter on the different triangles below:
Acute
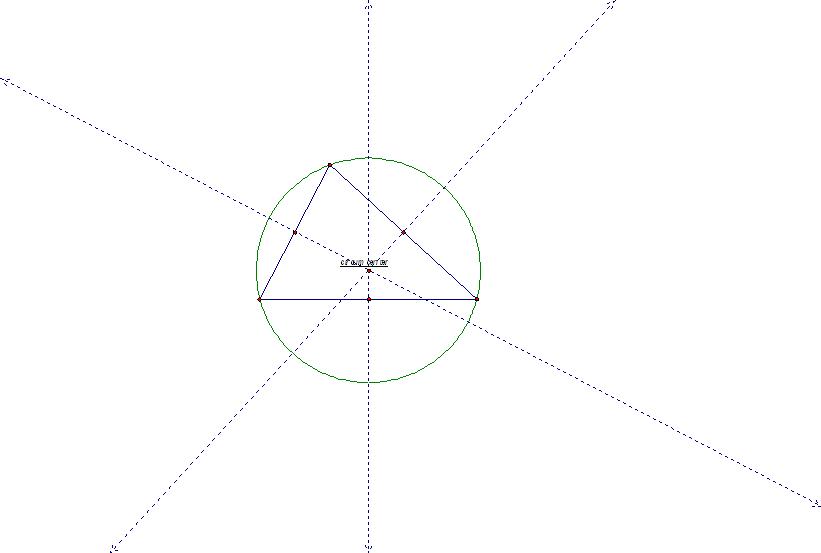
Obtuse
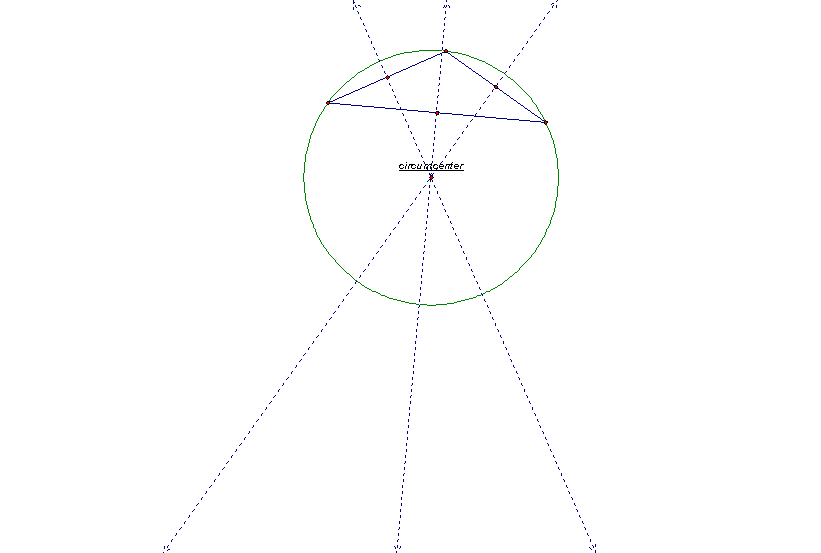
Right
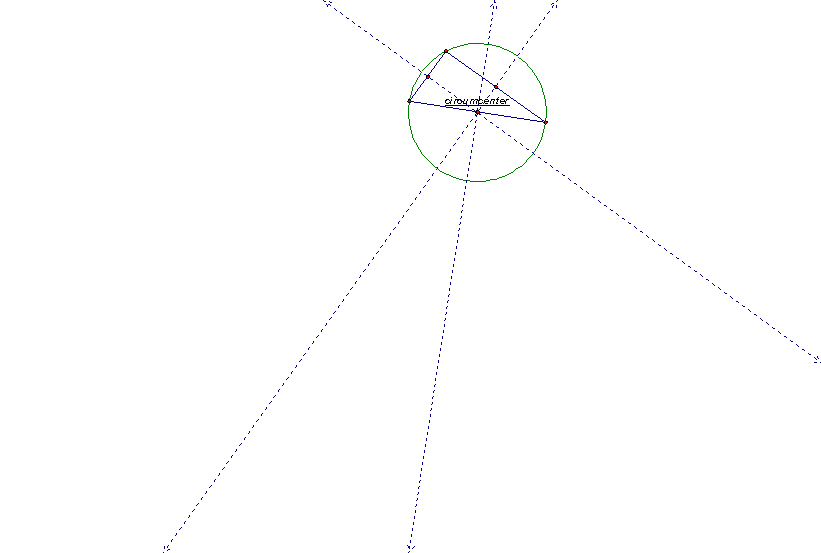
Equiangular
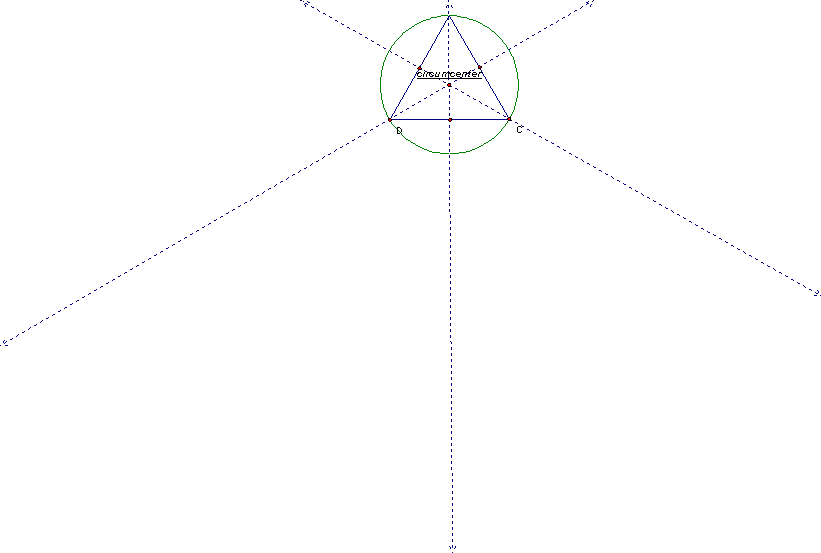
The circumcenter is the center of the circumscribed circle of the triangle. The distance from the circumcenter to any vertex of the triangle is the equal to the radius of the circle, because it is a radius.
The Incenter
An angle bisector is a segment that bisects an angle into two congruent angles. See an example of an angle bisector below:

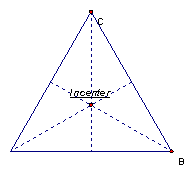
The incenter of a triangle is the point on the interior of the triangle that is equidistant from the three sides. Since a point interior to an angle that is equidistant from the two sides of the angle lies on the angle bisector, then the incenter must be on each angle bisector of the triangle. See the incenter in the different triangles below:
Acute
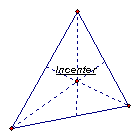
Obtuse
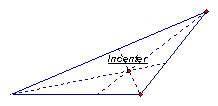
Right
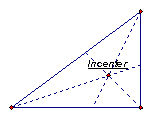
Equiangular
The incenter is the center of the inscribed circle of the triangle. See the figure below:
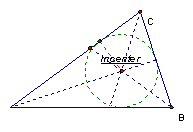
The radius is the red dashed line and was constructed by making a perpendicular line to one of the triangle legs.
Now that you have an understanding of the centers of a triangle, write an essay describing the centers in your own words and why you think they are called the centers of a triangle. Attach constructions of each center that your made yourself in GSP.