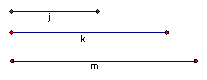
Problem #3. Given line segments j, k, and m. If these are the medians of a triangle, construct the triangle.

1. Construct a circle equal in radius to the shortest median.
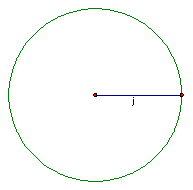
2. Let's call this circle one with the endpoints of line j labeled s and h for shortest median.

3. Construct a circle centered at Point S with the radius of the middle length median, line segment k.
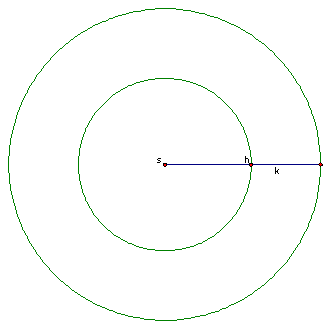
4. Let's call this circle two with the endpoints of the radius labeled s and m. s because it's the center and m standing for the middle median. :)
5. Construct a circle centered at h with the radius equal to the longest median.

6. Let's call this circle three with the endpoints of the radius labeled h and l. h because it is the center of the circle and l because it is the longest median.

7. Construct the intersection of the second and the third circle.

8. Let's choose the top intersection (it does not matter which one you choose) and label it point i for intersection.

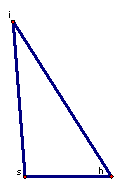
9. Construct line segments between s and h, s and i, and h and i.

Notice that line segment sh is the radius of circle one which is congruent to the shortest median, line segment si is the radius of circle two which is congruent to the middle median and line segment hi is a radius of the third triangle which is congruent to the longest median. We have successfully constructed a triangle given only it's medians. Look at the triangle below with all the circles and extra line segments hidden.