
1b. Click here for the general construction of a pedal triangle to triangle ABC where P is any point in the plane of ABC.
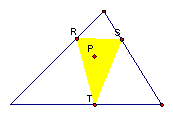
2. What if pedal point P is the centroid of triangle ABC?
When P is the centroid of the triangle the pedal triangle is
inside triangle ABC
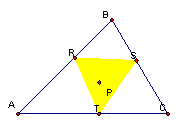
3. What if . . . P is the incenter . . . ?
When P is the incenter of triangle ABC, the pedal triangle is inside triangle ABC.
4. What if . . . P is the Orthocenter . . . ? Even if outside
ABC?
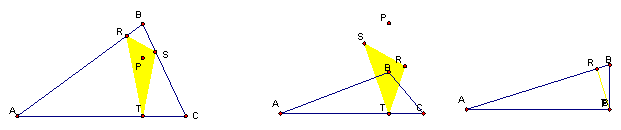
When P is the orthocenter of triangle ABC and is located inside the triangle, the pedal triangle is inside triangle ABC. When P is on the outside the pedal triangle overlaps triangle ABC. When triangle ABC is a right triangle, the pedal triangle collapses into a straight line.
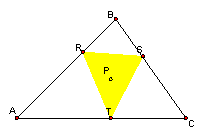
5. What if . . . P is the Circumcenter . . . ? Even if outside ABC?
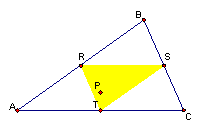
When P is the circumcenter, the pedal triangle is always inside the triangle. Even when P is outside the triangle.
6. What if . . . P is the Center of the nine point circle for triangle ABC?
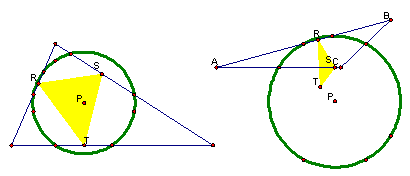
When P is the center of the nine point circle and is inside the triangle the pedal triangle is inside the triangle. When P is outside the triangle, the pedal triangle and triangle ABC overlaps.
7. What if P is on a side of the triangle?

When P is on the side of triangle ABC and the triangle is acute, the pedal triangle is inside ABC. When P is on the side of triangle ABC and the triangle is obtuse, the pedal triangle overlaps ABC. When P is on the side of triangle ABC and the triangle is right, the pedal triangle is also right.
8. What if P is one of the vertices of triangle ABC?
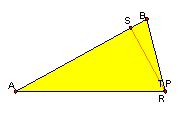
When P is on the vertex of triangle ABC, then the pedal triangle collapses into a straight line.
Click here in order to explore any of the above constructions in GSP. (Click on the bottom of the GSP page in order to see the various constructions)
When the three vertices of the Pedal triangle are collinear (that is, it is a degenerate triangle). This line segment is called the Simson Line. Which two cases above show the Simson line?