 2.
2. 
Introduction to Quadrilaterals
Geometry teachers in the Dekalb County School System are required to teach students the following regarding quadrilaterals:
recognize and define quadrilaterals, parallelograms, rhombi, rectangles, squares, and trapezoids
use the properties of parallelograms, rhombi, rectangles, squares, and trapezoids to solve problems
Defining & Recognizing Quadrilaterals
Students should visit http://www.techknowassociates.com/links/math.htm in order to define and find pictures of quadrilaterals, parallelograms, rhombi, rectangles, squares, and trapezoids. There are many sites students can choose from under this link. The student should decide which site to search from under this link in order to define and find pictures of quadrilaterals, parallelograms, rhombi, rectangles, squares, and trapezoids. Students are to turn in a write-up of their findings. Students should click here in order to fill out the write-up. When students are finished, they should print out their write-up (remind students not to forget to type their name before printing) and share what they have found with their classmates. Students should be prepared to demonstrate any drawing on the overhead or board.
Properties of Parallelograms, Rhombi, Rectangles, Squares, and Trapezoids
Construct the following in GSP or on a TI-92 calculator:
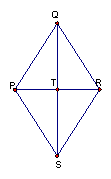
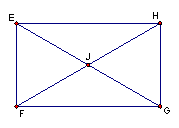
Label each quadrilateral ABCD and the diagonals intersection E. If the students do not know how to construct the quadrilaterals, they may simply click on the name of the quadrilateral they need help with above. Each shape is linked to it's own GSP construction. In order to see the hidden objects in the construction, go to display and show all hidden on the menu bar in GSP. (Do not let students copy and paste into their file. Students must construct it themselves following the directions in the file.) After following the directions in the file, students should then open their own document and construct their own.
After constructing our special quadrilaterals, have students use the measuring capabilities of GSP or the TI-92 calculator in order to explore the characteristics of each quadrilateral above. Measure every angle, side, diagonal and diagonal part of each quadrilateral. Click here in order to record your findings and answer questions for this investigation.
Median of a Trapezoid
Construct the median of a trapezoid in GSP or using a TI-92 calculator.
Step 1: Draw a trapezoid of any shape or size. Label the vertices ABCD with legs line segment AD and line segment BC.
Step 2: Construct the midpoint of line segment AD and line segment BC. Label the midpoints M and N.
Step 3: Construct line segment MN.
Measure line segments AB, DC, and MN. Add AB and CD. Compare the sum of AB and CD to MN. What do you observe about the lengths?
Click here in order to see my GSP construction.
Reflections
Locate your very first write up about quadrilaterals. Look at question number 3. Were your conclusions from your definitions consistent with your investigation of the properties for quadrilaterals? Type a reflection paper about the situations in which you were correct and incorrect. Email the paper to me.
Using Properties of Parallelograms, Rhombi, Rectangles, Squares, and Trapezoids to Solve Math Problems
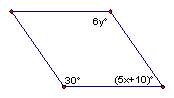
Find the values of x and y to ensure each quadrilateral is a parallelogram.
1.
 2.
2. 
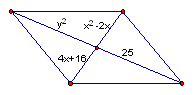
3. The quadrilateral below is a rhombus. Find the values of x and y if PT = 4x-8, QT = 6y-9, TR=16 - 2x, and TS = 3y+9. What is the measure of angle STP?
4. Quadrilateral EFGH is a rectangle. Find the value of x if JF = 8x + 4 and EG = 24x - 8.
5. Determine whether quadrilateral KLMN with K(12,0), L(6,-6), M(0,0), and N(6,6) is a parallelogram, a rectangle, a rhombus, or a square. List all that apply and justify your reasoning.
6. The measures of the bases of a trapezoid are 22 and 28. What is the measure of the median of the trapezoid?
See more quadrilateral problems by visiting the book site that Dekalb County adopted.
When will we ever use this?
A deed is a legal document that not only indicates the seller and buyer of a plot of land, but also provides a mathematical description of the land whose ownership is being transferred. Often the description includes lengths and directions from known landmarks that define the boundary of the property. Legal Assistants, lawyers and realtors are a few professional people who need to know how to read and comprehend these legal documents.
Classify the plot of land you see in the documents below. The 1st is a document focusing on one house. The second document is of a neighborhood. How many quadrilaterals do you see? Describe each plot of land as specifically as you can. You can look at the documents in GSP by clicking on the link underneath the document, if that will help you decide.
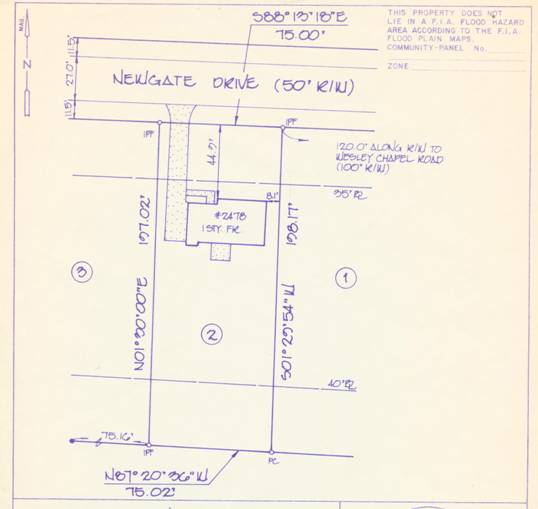
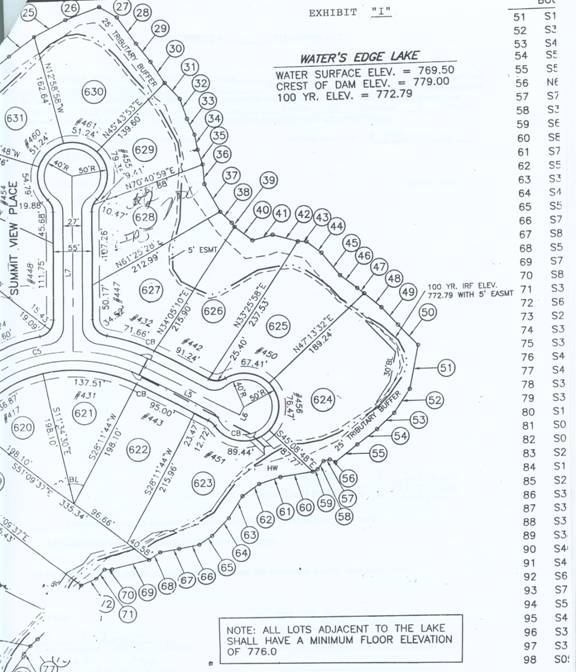
Land Lots for part of a neighborhood
Being familiar with geometry will make it easier for people to understand these documents. Can you think of any other situations where knowing the definition of a quadrilateral, the different types of quadrilaterals, and the properties of various quadrilaterals might be useful? Write them down. Then research those topics (using the internet, interviews with people in that field, etc.) in order to see if your conjectures were right. Report your findings back to the class by the end of the week.
Project - Quadrilaterals in Sports
found in Glencoe Geometry Investigations and Projects Masters
1. Playing fields, much sports equipment, and play in general involve the use of quadrilaterals. List as many sporting events as you can that use quadrilaterals. Also, list the types of quadrilaterals involved in each sport.
2. Compile a list of the quadrilaterals found in each sport by the entire class, as well as a list of the types of quadrilaterals involved.
3. Work in small groups to design a game with a playing field that uses at least three of the following types of quadrilaterals: parallelogram, rectangle, square, rhombus, and trapezoid. Make rules for your game and explain how it uses each quadrilateral.
4. Present you game to the class.
5. After presentations, we will vote on the best game and play it outside for Fun Friday!
6. Write a one page paper about the game. Was it as fun as you thought it was going to be? How did it compare to the game you made? Was it competitive? Did it involve quadrilaterals? What do you think the grade on this game should be?