Final Assignment
EMAT 6680, Final, Fall 2004
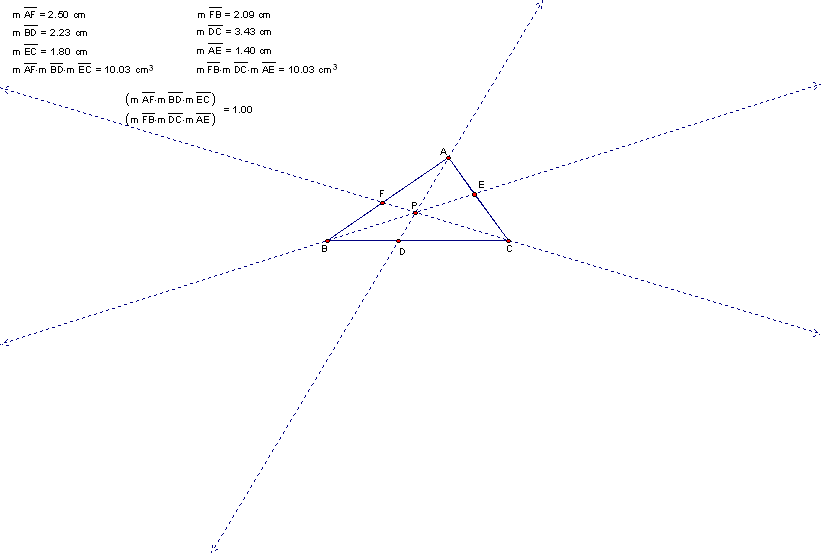
Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively. Explore (AF)*(BD)*(EC) and (FB)*(DC)*(EA) for various triangles and various locations of P, including cases where P is located outside the triangle. Show a working GSP sketch.

From the example above, it seems as if (AF)*(BD)*(EC) and (FB)*(DC)*(EA) are congruent to each other and that ((AF)*(BD)*(EC)) / ((FB)*(DC)*(EA)) = 1. Does the same thing happen when P is located outside of the triangle?
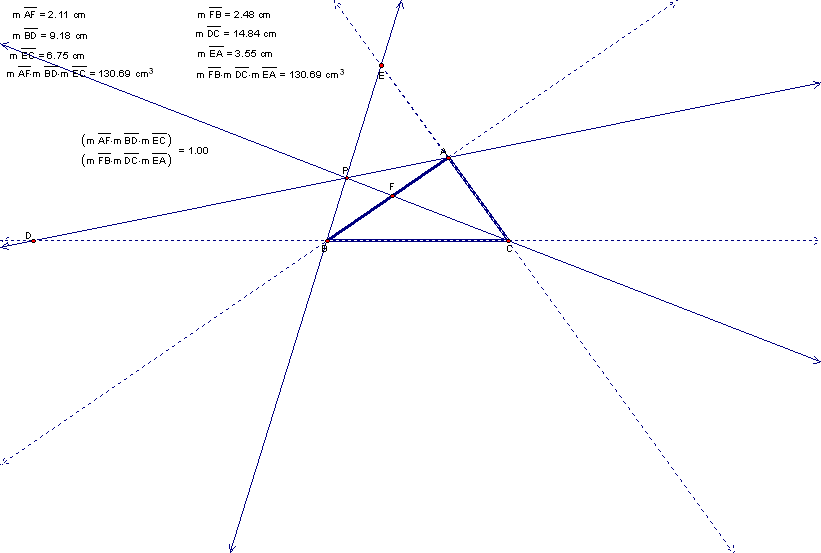
It looks like it works for the outside of the triangle too! Try for yourself. Click here for a working sketch. Now let's prove this!
First, construct a line through A that is parallel to line BC. Construct the intersection of the parallel line with CF and BE. Name the intersection H and I, respectively. Triangle AIE ~ Triangle CBE by AA similarity. Angle AEI is congruent to angle CEB because they are vertical angles. Angle ECB is congruent to angle EAI because when two parallel lines are cut by a transversal, alternate interior angles are congruent.
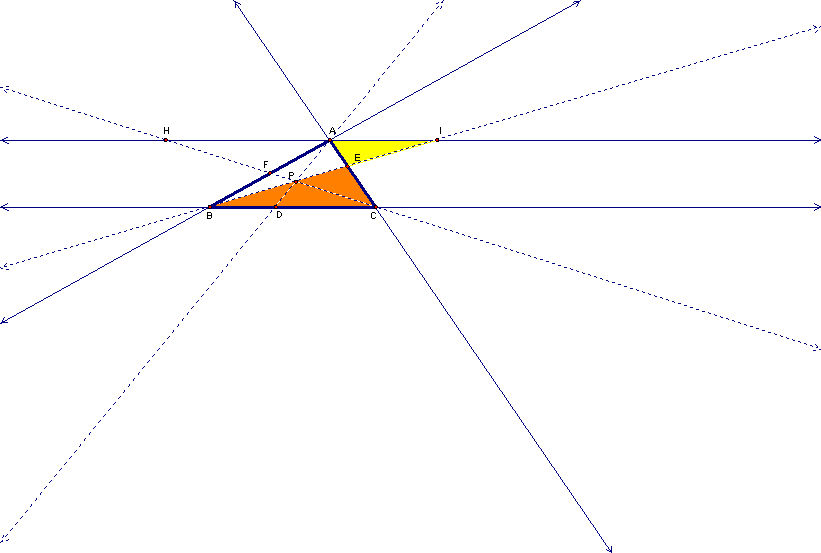
Since these triangles are similar we know that AE/EC = AI/BC.
The same logic can be used to determine that triangles AFH and CBF are similar. So we can say that BF/AF = CB/AH.
The same logic can be used to determine that triangles AHP and CDP are similar. So we can say that AH/CD = AP/DP.
The same logic can be used to determine that triangles BDP and AIP are similar. So we can say that AI/DB = AP/DP.
Since AH/CD = AP/DP & AP/DP = AI/DB, then AH/CD = AI/DB by the transitive property. By cross multiplying and dividing, AH/CD = AI/DB can be written as CD/DB = AH/AI. Now let's look at all the ratios we have. AF/FB = AH/CB, BD/CD = AI/AH & CE/AE = BC/AI. So, ((AF)*(BD)*(EC)) / ((FB)*(DC)*(EA)) = ((AH)*(AI)*(BC))/((BC)*(AH)*(AI)). Everything on the right hand side of the equation cancels out, and we are left with ((AF)*(BD)*(EC)) / ((FB)*(DC)*(EA)) = 1. It's proven!
Show that when P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4. When is it equal to 4?
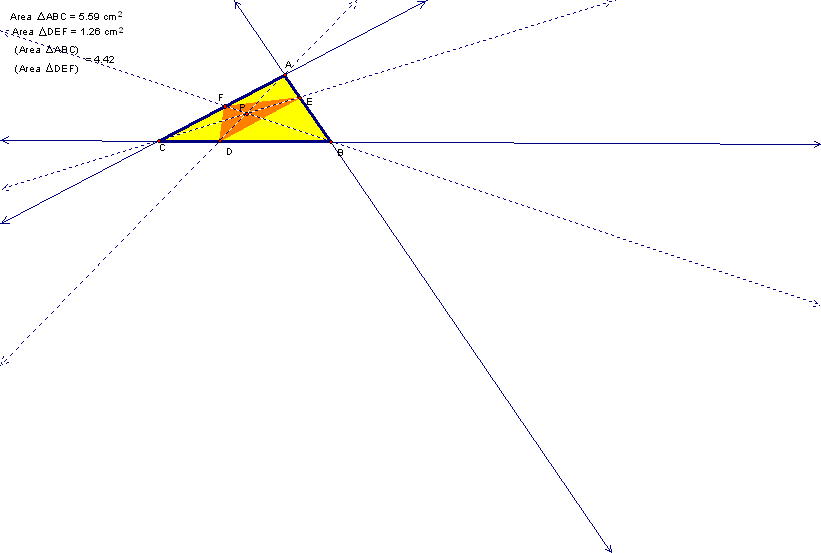
Click here in order to move P around in GSP and see for yourself that the ratio of the area of triangle ABC and triangle DEF will always be four or greater.
The ratio will always be equal to four when P is the centroid. The medial triangle is always 1/4 of the area of the original triangle. The medial triangle is constructed by connecting the midpoints of the sides of the triangle. The intersection of the medians is the centroid, thus when P is the centroid a medial triangle is formed. Click here in order to see a construction of a medial triangle.