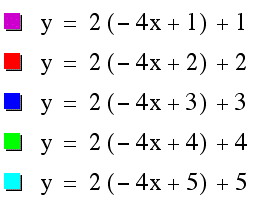Exploring the linear functions
Problem 2
Make up linear functions f(x) and g(x). Explore, with diffefent pairs of f(x) and g(x) the graphs for
1.) h(x) = f(x) + g(x)
2.) h(x) = f(x).g(x)
3.) h(x) = f(x)/g(x)
4.) h(x) = f(g(x))
Summarize and illustrate.
Let's make up the linear functions such as f(x)=ax+b and g(x)=cx+d.
Algebraically, we can simplify as below:
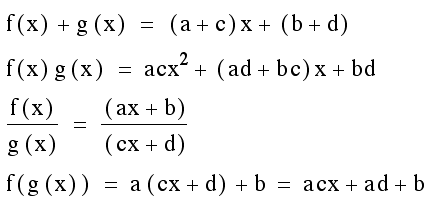
The addition and composition of the two linear functions are linear equations, and the multipication is
the quadratic equation. In the case of division, we can observe that there is an asymptote at x=-d/c.
Here are some examples.
Let f(x)=2x+b and g(x)=-4x+d where b and d are 1,2,3,4,5.
Case 1) f(x)+g(x)
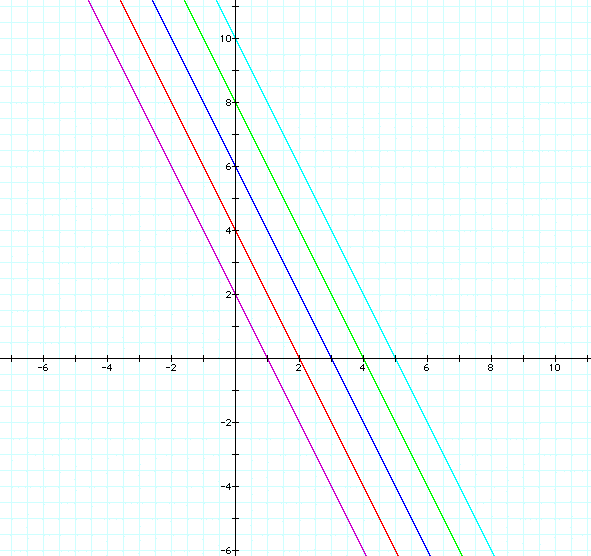
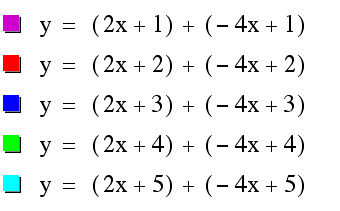
Case 2) f(x).g(x)
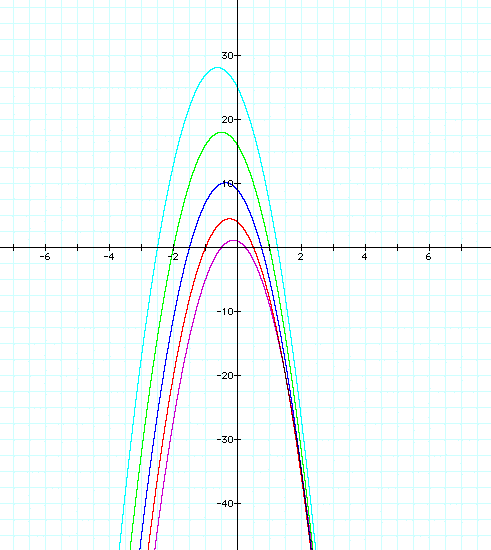
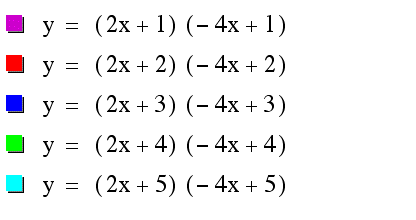
Case 3) f(x)/g(x)
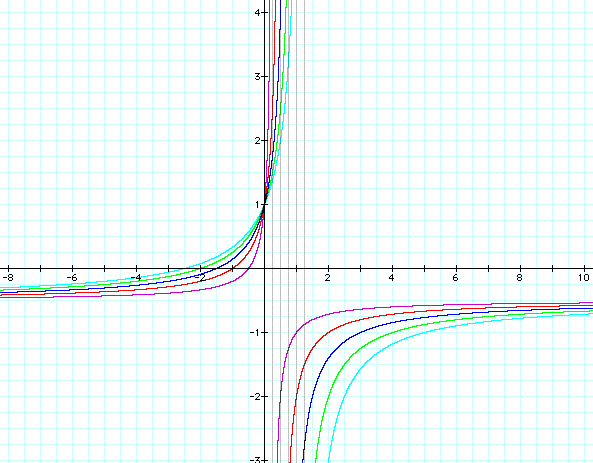
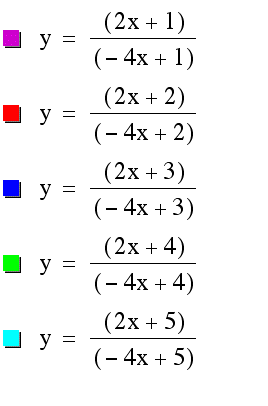
Case 4) f(g(x))