Investigations with spreadsheets
The spreadsheet is a utility
tool that can be adapted to many different explorations, presentations,
and simulations in mathematics. There are spreadsheets available
on almost any platform. An essential feature should be the ability
to make graphs and charts from the matrix of data. Try using a
spreadsheet, such as EXCEL or ClarisWorks, for some of the following
investigations.
Let's explore the Fibonacci sequence and Lucas sequence using Excel.
The first few Fibonacci numbers are 1, 1, 2, 3, 5, 8, 13, 21, ...
To generate the Fibonacci sequence, input only the first two numbers to A2 cell and A3 cell and type "=A2+A3" in the A4 cell. Here I used the A1 cell for the label. After that, drag the A4 cell for the generating the same scheme. Then you will get the Fibonacci sequence.
In the Fibonacci sequence (0, 1, 1, 2, 3, 5, 8, 13, ...), each term is the sum of the two previous terms (for instance, 2+3=5, 3+5=8, ...). The second column shows the ratio of f(n)/f(n-1). It is the ratio of each pair of adjacent terms in the Fibonacci sequence. The third column is the ratio of f(n)/f(n-2), and so on. As n is increasing, what happens the ratio of each columns?
As you go farther and farther
in this sequence, the ratio of a term to the other will get closer
and closer to certain numbers, which is the limit.
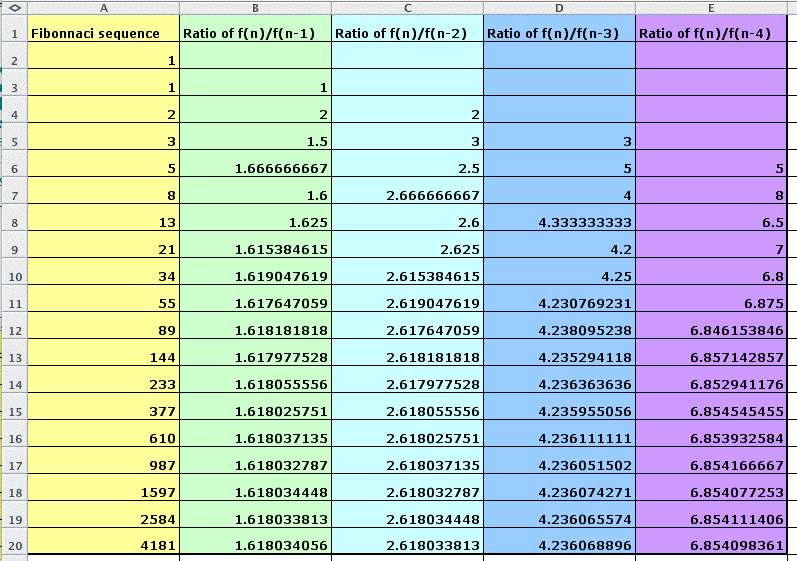
If f(0)=1 and f(1)=3, then the sequence is a Lucas sequence. I generate the Lucas sequence with the Excel. Here we can observe the ratio of each column has the same limit as Fibonacci sequence.
Now, let's talk about the Golden Ratio.
The golden ratio is a special number approximately equal to 1.618033... We use the Greek letter Phi to refer to this ratio. Like Pi, the digits of the Golden Ratio go on forever without repeating. It is often better to use its exact value:
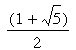
Take a line segment and label its two endpoints A and C. Now put a point B between A and C so that the ratio of the short part of the segment (AB) to the long part (BC) equals the ratio of the long part (BC) to the entire segment (AC):
The ratio of the lengths of the two parts of this segment is the Golden Ratio. In an equation, we have
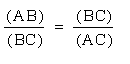
If we set the value of AB to be 1, and use x to represent the length of BC, then
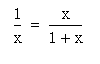
i.e.,
Thus, the zero of the equation
is the value given above, 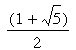, 1.618033... Can
you tell this value is same as the limit of the ratio of f(n)/f(n-1)?
Can we verify the following?
From the equation
,
we have
= 1.6180339887498948482 + 1
= 2.6180339887498948482.
How about 4.23606798?
