Centers of a triangle

1. Use Geometer's Sketchpad (GSP) to Construct the centroid and explore its location for various shapes of triangles.
------------------------------------------------------------------------
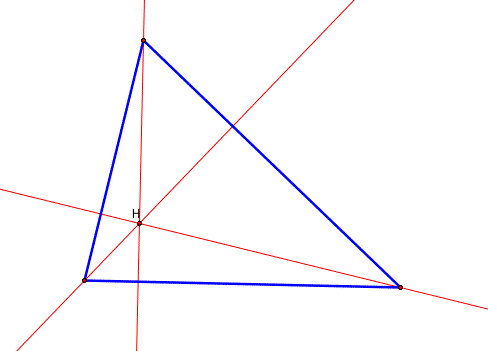
2. Use GSP to construct an orthocenter H and explore its
location for various shapes of triangles. (Make sure your construction
holds for obtuse triangles.)
------------------------------------------------------------------------
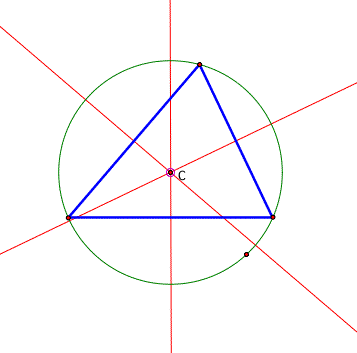
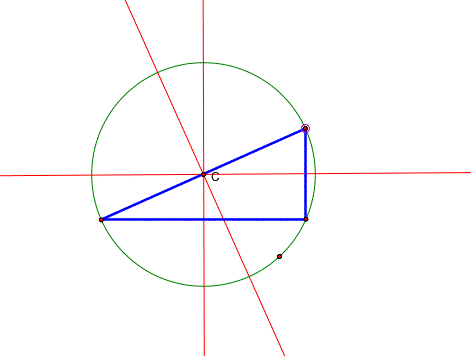
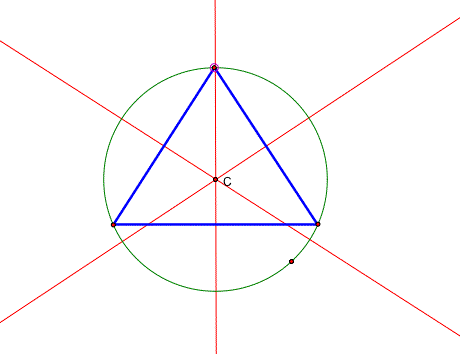
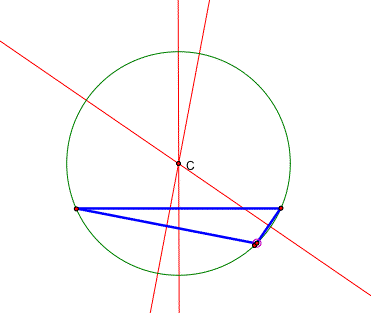
3. Construct the circumcenter C and explore its location
for various shapes of triangles. It is the center of the CIRCUMCIRCLE
(the circumscribed circle) of the triangle.
The centroid of a triangle is the common intersection of three medians. A median of a triangle is the segment from a vertex to the midpoint of the opposite side. Here, D,E,F are the midpoint of each segment BC, AC, and AB. G is the point of intersection of AD, BE, and CF and it is called the centroid of a triagle ABC.
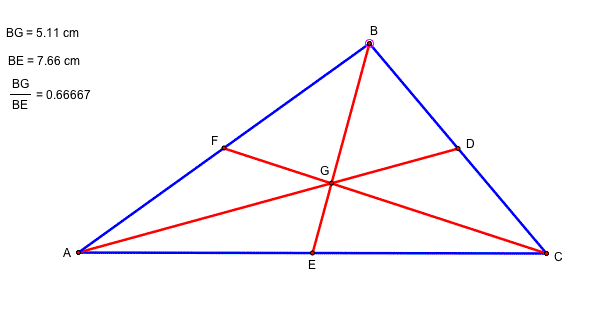
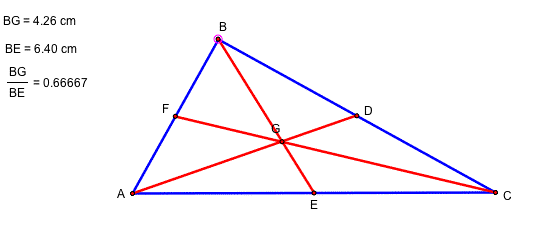
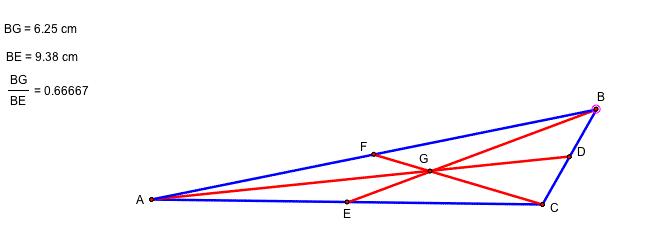
The centroid is two-thirds the distance from each vertex to the opposite side. For example, BG=(2/3)(BE).
By dragging one of the vertex, triangle ABC is moving with different values of BG and BE. However, the rate of the BG/BE is a constant.
To play with this on the Geometer's Skethchpad, please click here.
The ORTHOCENTER (H) of a triangle is the common intersection of the three lines containing the altitudes. An altitude is a perpendicular segment from a vertex to the line of the opposite side.
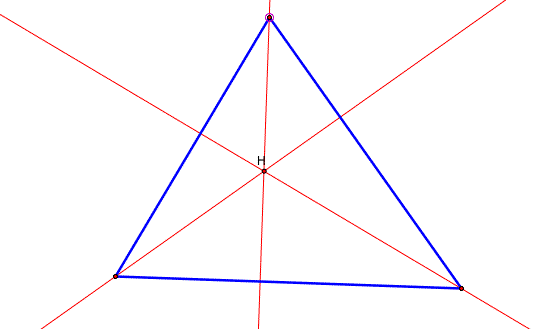
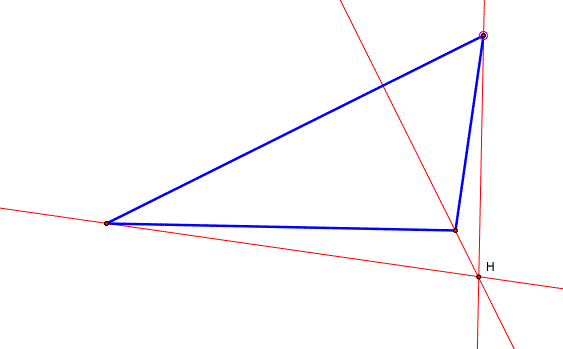
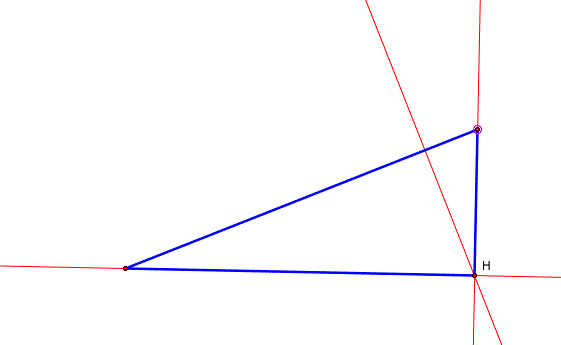
The CIRCUMCENTER (C) of a triangle is the point in the plane equidistant from the three vertices of the triangle. Since a point equidistant from two points lies on the perpendicular bisector of the segment determined by the two points, C is on the perpendicular bisector of each side of the triangle.