Problem 11.. Consider any triangle ABC. Find a construction for a point P such that the sum of the distances from P to each of the three vertices is a minimum.
Let's take the triangle as follows: the vertices are A(2,3), B(0,0) and C(4,0).
Here is the triangle I draw using GSP. To have the GSP file, please click here.
Move the point P, and try to find the minimum of the sum AP+BP+CP.
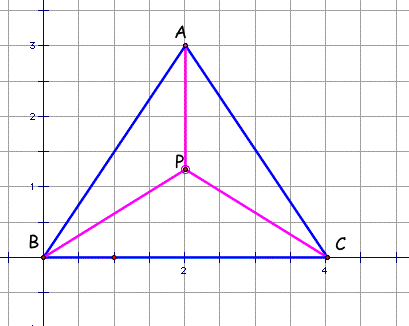
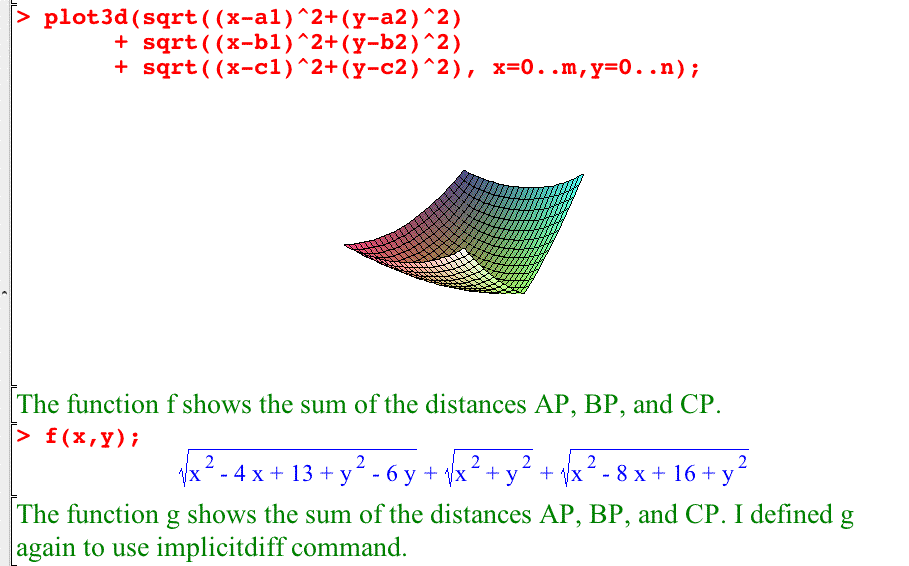
How can we find the x, y - coordinates of the point which the sum AP+BP+CP is minimum.
With GSP, it is easy to estimate the point P, but it is impossible for me to find the exact coordinates of P. I investigete this problem with Maple here.




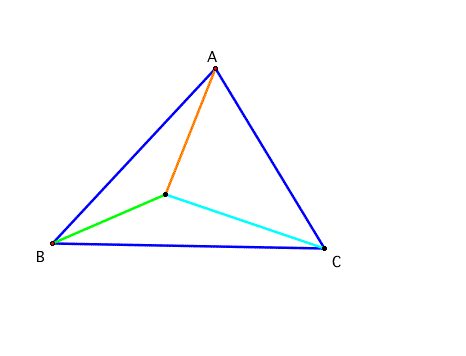
After I struggled to find the point P, I was surprised by the Dr. Wilson's explanation with GSP. It was really simple and understandable even though you don't know calculus. What a good idea!
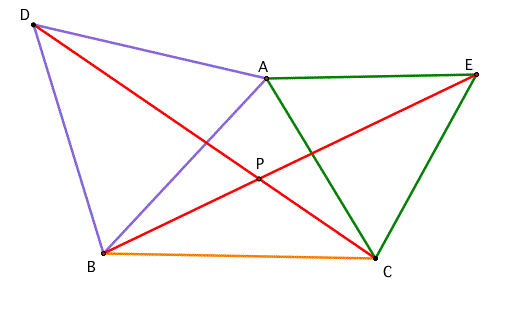
First of all, let's construct the triangle ABC and pick one point inside of the triangle. Draw the segments from the each verticle to the point.
Then, let's rotate the left side part of the triagle by 60 degree to the left.
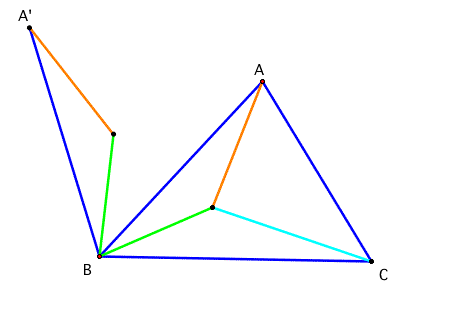
The angle between two green segments is 60 degree and the length of both segments is equal. By constructing a line segment between two points we can get the equilateral triangle. So..... What is the idea to get the minimum length? Yes! Have the straight line to A' to C.
The point of P will be on the red line segment A'C.
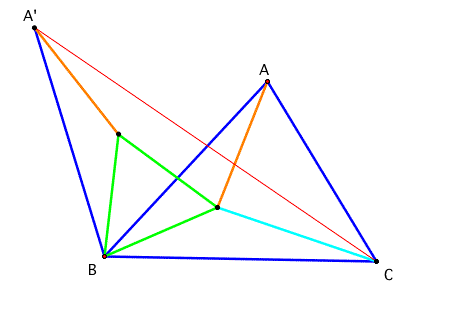
Can we repeat the process with the right side part of the triangle? The point of intersection of both red lines will be the point P which the sum of AP, BP, and CP is the minimum.
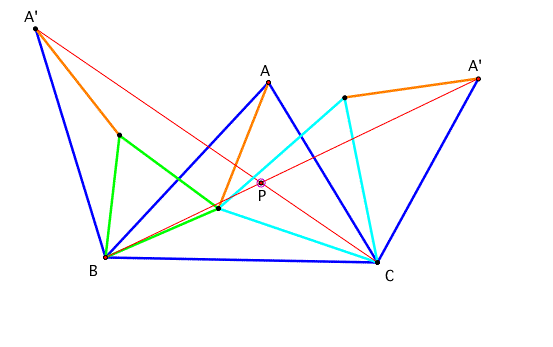
This whole process can be summerized like this: For any triangle, construct the equilateral triangles each side and connect the line segment. The point of intersection has the minimum length of the sum AP,BP, and CP. I've learn this is called Fremat triangle and Fermat point.