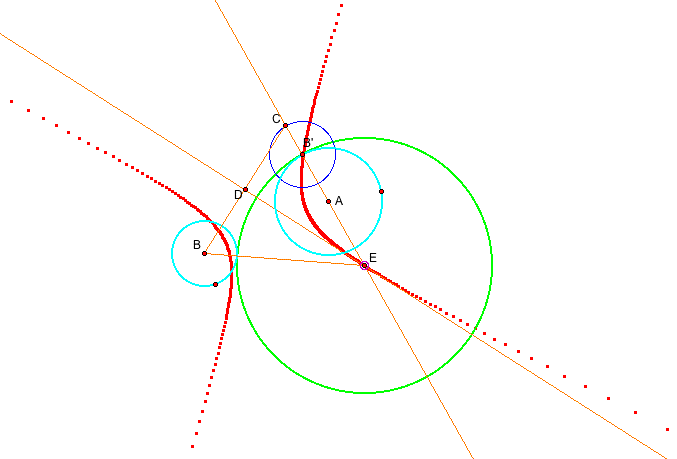
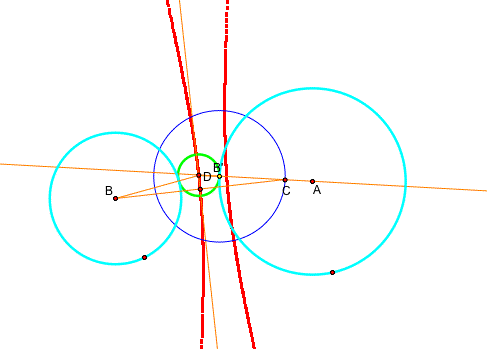
CASE 1
Let's start the following problem : Construct a circle tangent to the given two circles.
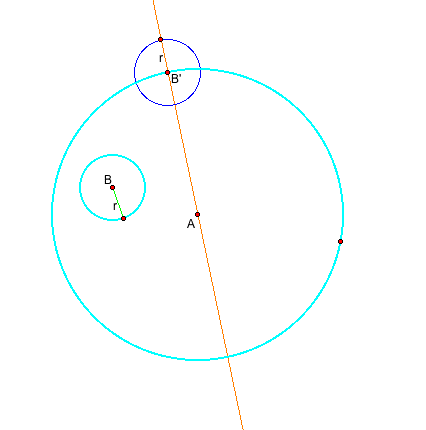
First of all, draw a line passing through the center of the one circle. Let's call B' the point of the intersection between the circle and the line. Then, measure the radius of the other circle and draw a circle with the same radius at the point B'.
Next, take the point c, which is the point of intersection between the line AB' and the new circle. Construct the segment BC.
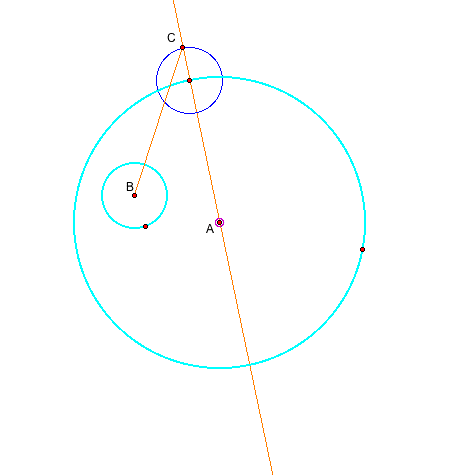
After that, find the midpoint D between the segment BC.
Now, draw a pependicular line at D on the segment BC.
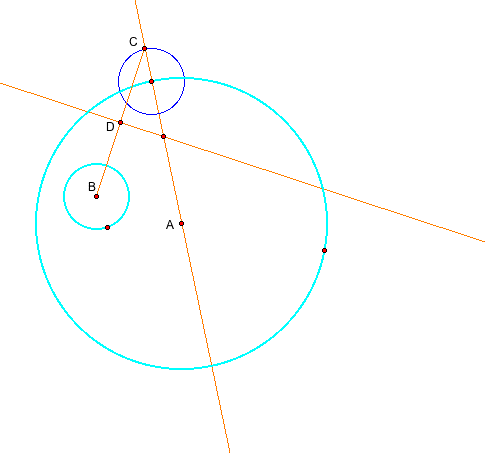
Can you find the point E? It is the point of intersection between two lines. The point E is the center of the circle tangent to the given two circle. Take the radius from E to B' and consturct a tangent circle.
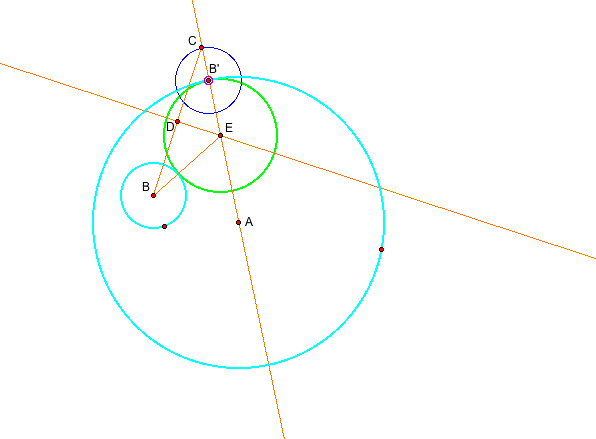
Here is the GSP file. Click here and explore the tangent circles. Get the animation to see the trace of the center of the tangent circles.
Do you see an ellipse?
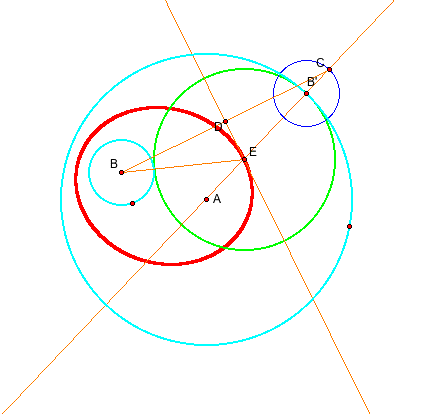
CASE 2
Let's think about the other cases?
If two given circles intersect, we can construct the tangent circle as below. Guess what the trace of the center of the tangent circles is? Yes, we have an ellipse again in this case.
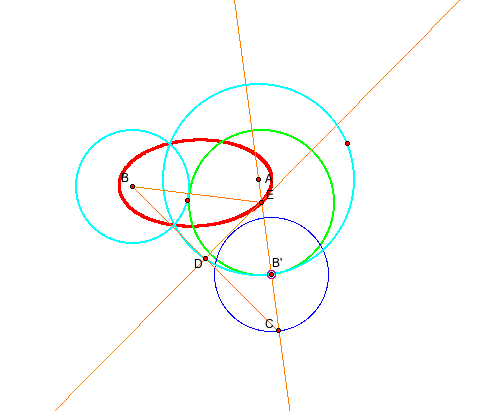
However, can we cover all tangent circles? No. We need to investigate the case below. Here the trace is a hyperbola.
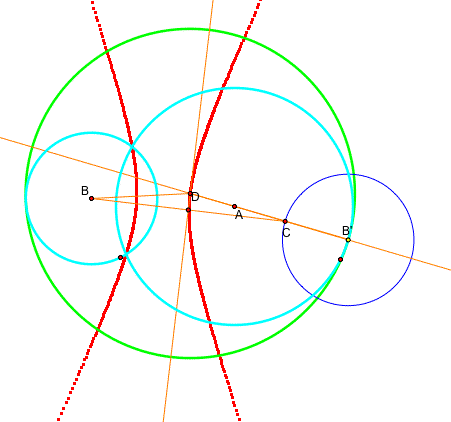
CASE 3
Well, now let's look at the tangent circles when two given circles are disjoint. We can generate two animaitons. In the first one, the trace of the center of the tangent circles is the hyperbola while as we have the ellipse in the second animaiton.