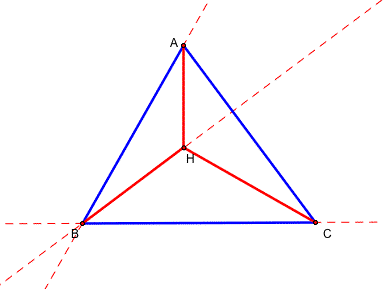
Construct any triangle ABC. Then drop the perpendicular lines from each verticle A,B, and C to the opposite sides. Take the orthocenter H of the triangle ABC.
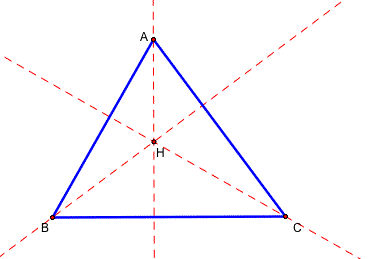
Now, construct the orthocenter of the triangle HBC. We need to drop the perpendicular lines from H,B, and C to the opposite side. From the following figure, A is the orthocenter of the triangle HBC.
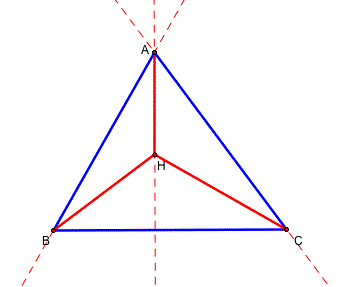
The next step is finding the orthocenters of the triangle HAB and HAC. Can you guess what they are? Yes. C is the orthocenter of the triangle HAB and B is the orthocenter of the triangle HAC.
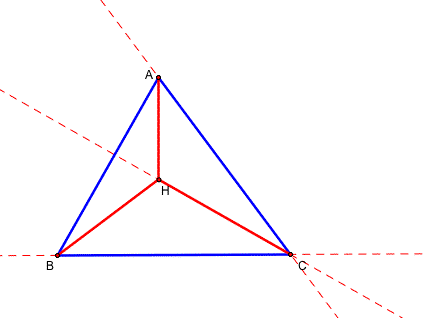
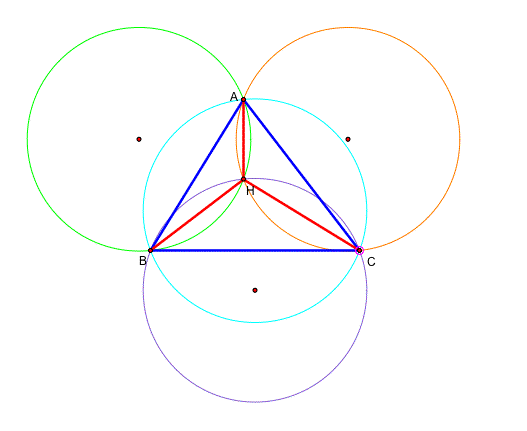
After that, let's construct the circumcicles of triangles ABC, HBC, HAB, and HAC.
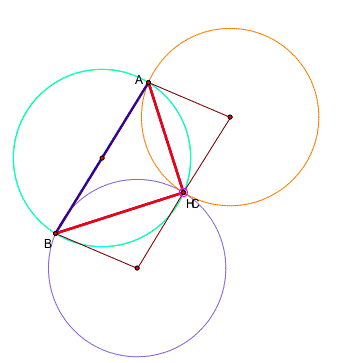
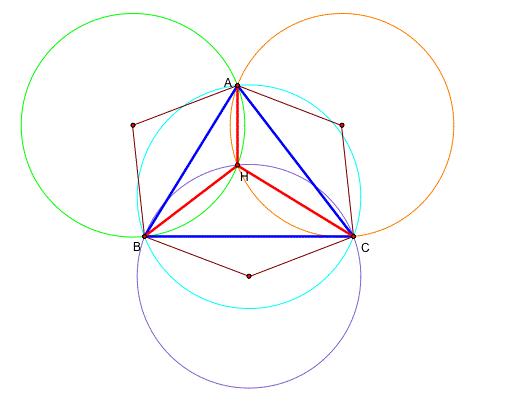
Can we find some intersting figure here? Let's consturct segments between the circumcenters of the triangles and the vertices of the triangle ABC. Here we go! If you want to see GSP file, please click here.
What would happen if the vertex C of the triangle ABC was move to where the orthocenter H is located? Now, we have a rectangle instead of hexagon. To see animation, please open this GSP file and click the animation button.