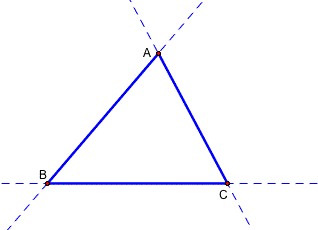
Let's construct a pedal triangle. Let triangle ABC be any triangle. Draw the triangle ABC and extend the each side using dotted lines.
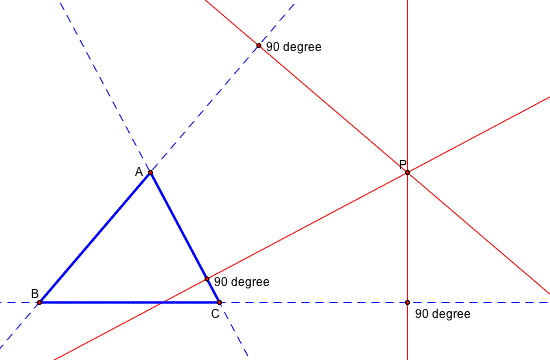
Then take any point P in the plane. Construct the perpendicular lines to the each side of ABC on the point P.
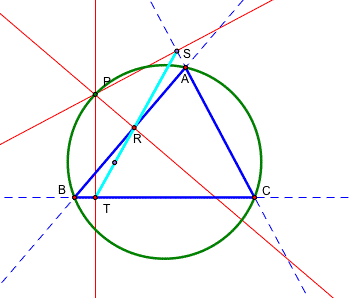
ow, let's take the midpoints of the each side of RST. Then draw a circle and merge the padal point P on the circle.
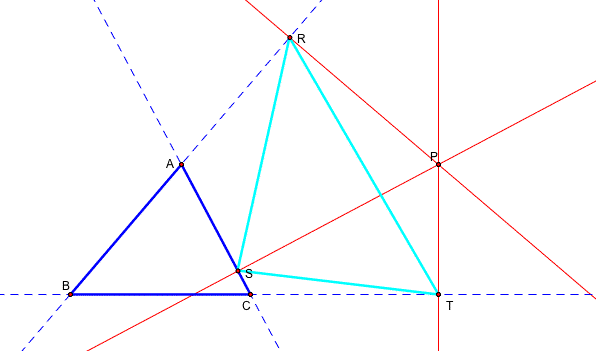
Now find the triangle RST by constructing the segments connecting three points R,S, and T which are the points of intersection between the pependicular lines and the extended sides of the triangle ABC.
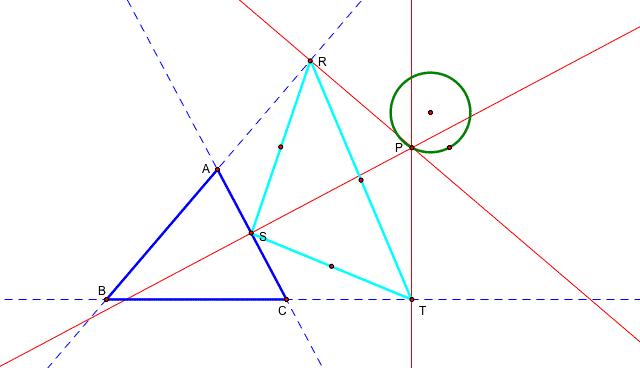
Move the padal point P around the green circle. Let's draw the trace of the midpoints of each side of RST. Here we get three ellipse for the each midpoint by moving the padal point P around the circle.
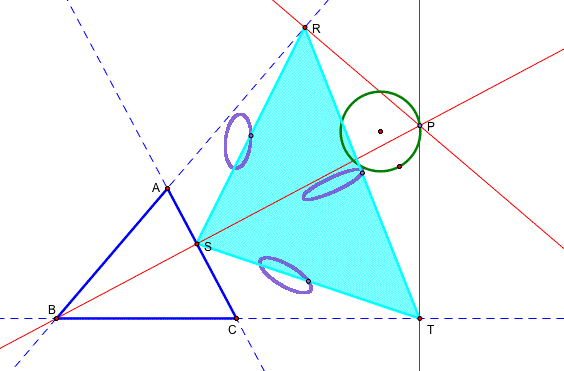
Let's investigete the patal curves. Now construct the circumcircle of the triangle ABC. Then move to the padal point on the curcumcircle. What are you expecting in this case? Can we have the same trace of the midpoints?