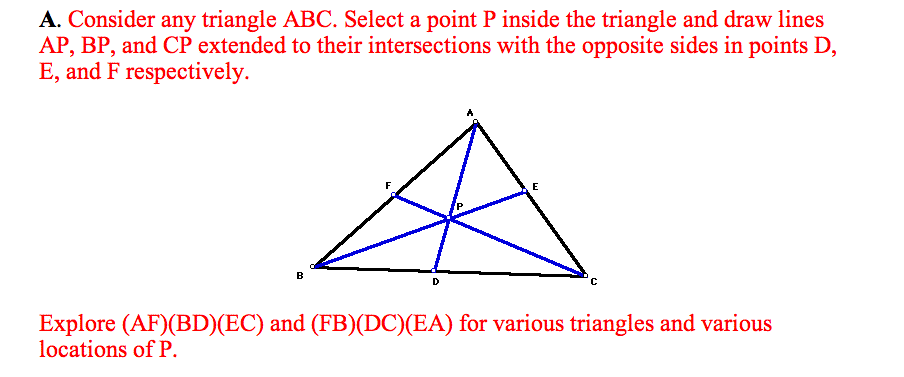
Here, I explored (AF)(BD)(EC) and (FB)(DC)(EA) for the different four triangles and different locations of P by using GSP. If you want to see GSP file, please click here.
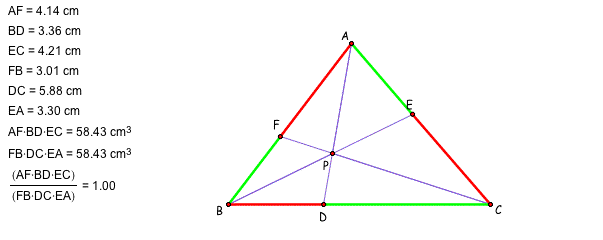
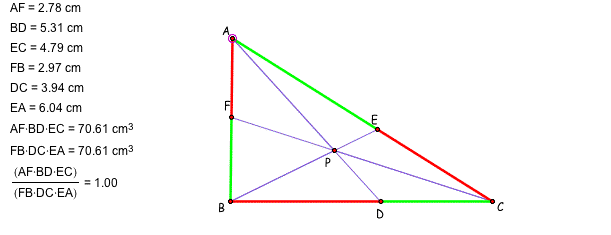
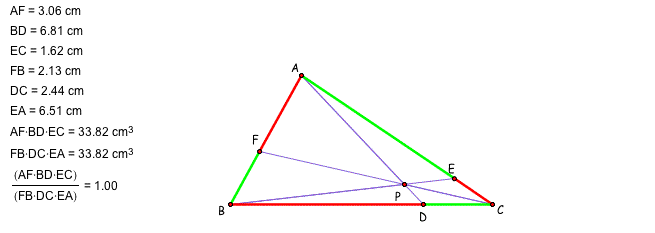
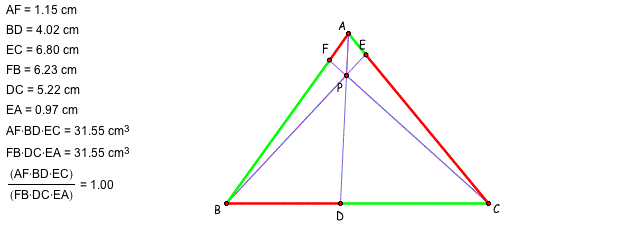

From the GSP exploring, we may have a conjecture such that the ratio of (AF)(BD)(EC) and (FB)(DC)(EA) is 1. How can we prove this? We will talk about the ratio between the segments in the triangles. Can we have any similar triangles? Let's add the parallel line and try to find the similar triangles.
After constructing a triangle ABC, draw the parallel line to BC passing through A. Then let's extend the line CF and BE. Let G and H be the points of intersection. We will consider the four pairs of the similar triangles and find the relationship between the ratio of the segments of the triangles.
First of all, let's look at the orange triangles PBD and PHA.
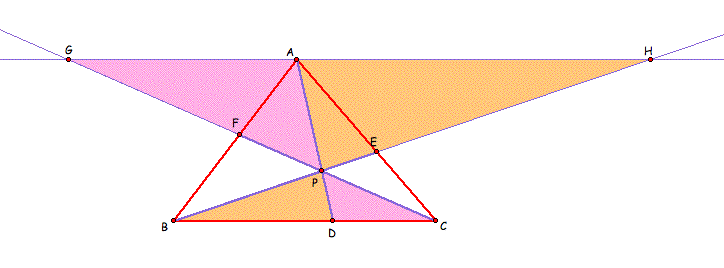

We have the similarity in the pink triangles PCD ad PGA.

Now, consider the following similar triangles. First, look at the yellow triangles FBC and FAG.
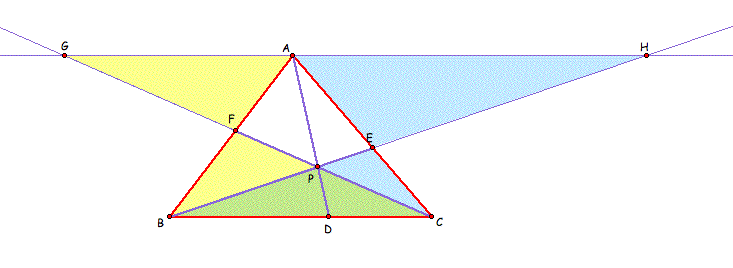
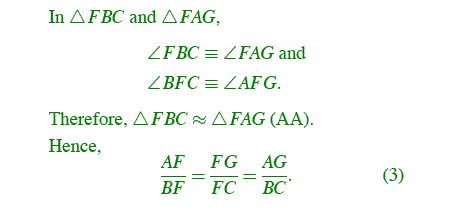
Also, we have the same relationship between two blue triangles EBC and EHA.
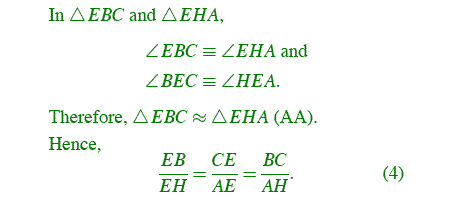
From (1),(2),(3),and (4), we have the ratio of (AF)(BD)(EC) and (FB)(DC)(EA) as follow:

This result can be generalized when the point P is outside the triangle. The next two figures show that the ratio of (AF)(BD)(EC) and (FB)(DC)(EA) is 1. Click here for the GSP file.
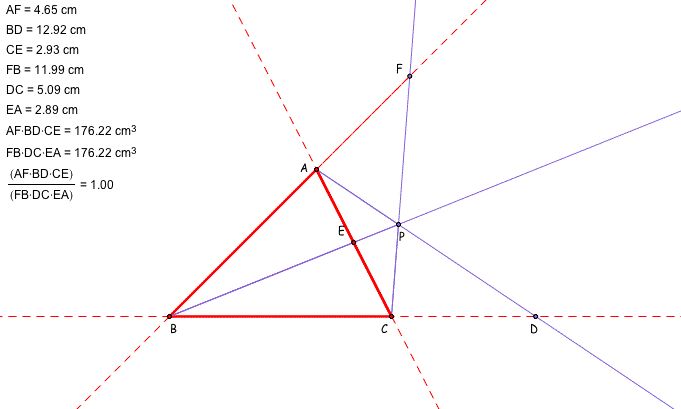
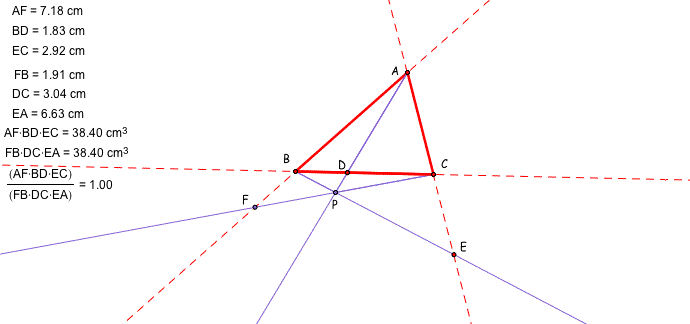
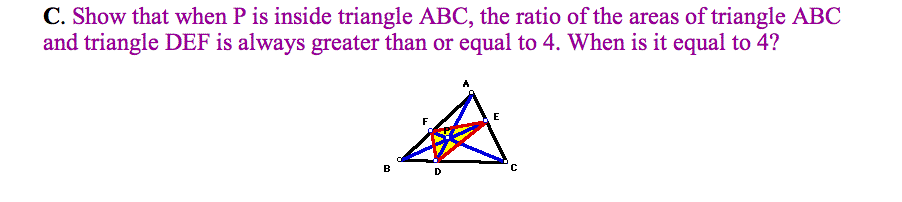
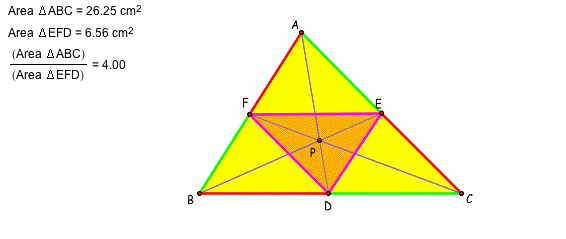
Using GSP, let's explore the ratio of the area ABC and DEF. Please click here to open the GSP file and move the vertices A, B, or C and the point P. We can see the ratio is always greater than or equal to 4 in the various triangles and the point P.
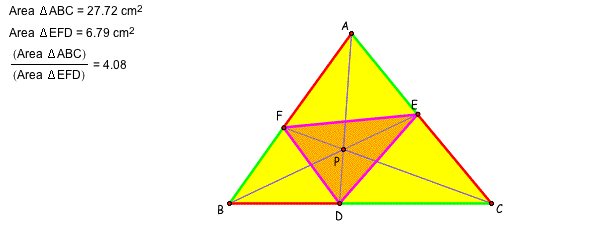
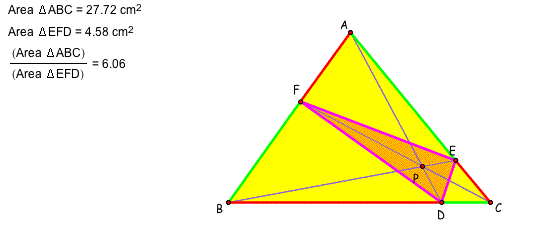
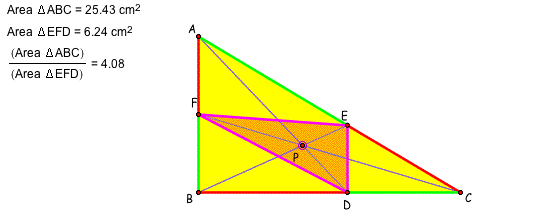
In the following case, the point P is the centroid of the triangle ABC. The triangle DEF is similar to the triangle ABC. Every segment of the triangle DEF is 1/2 of the triangle ABD. Hence, area of the triangle DEF is 1/4 of the triangle ABC.