A. Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.

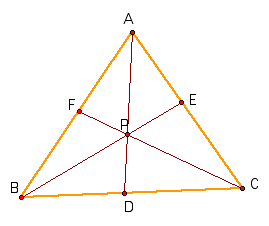
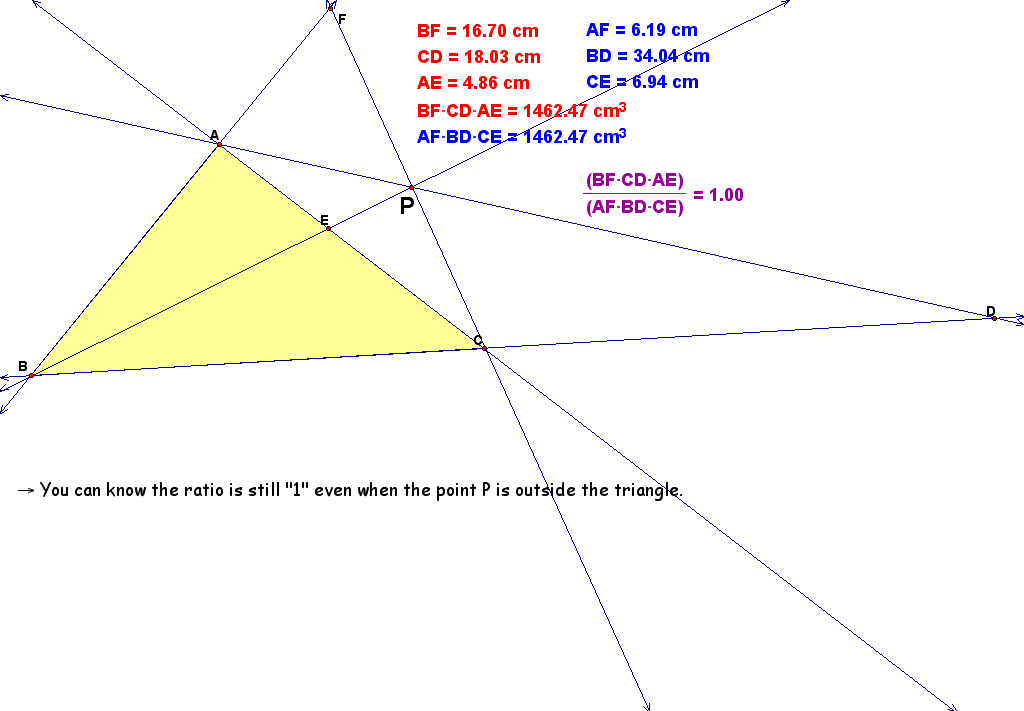
Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P.

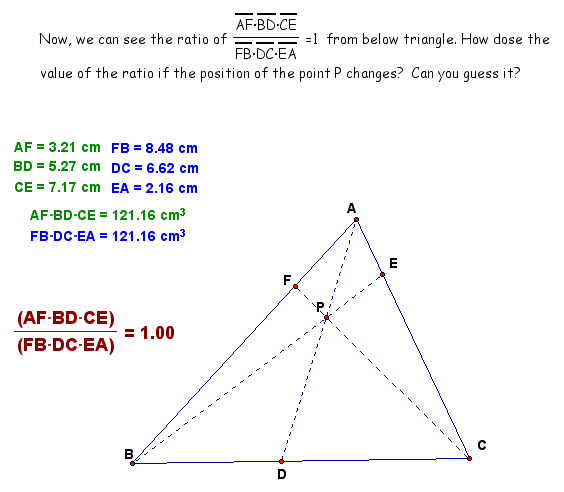
At first, let's look at the change of the point P

Click here!!!!

Secondly, let's loot at the change of the shape of the triangle. Click here!!!!

B. Then, If you draw the pararell line HG, you can find many pairs of similar triangles as follows.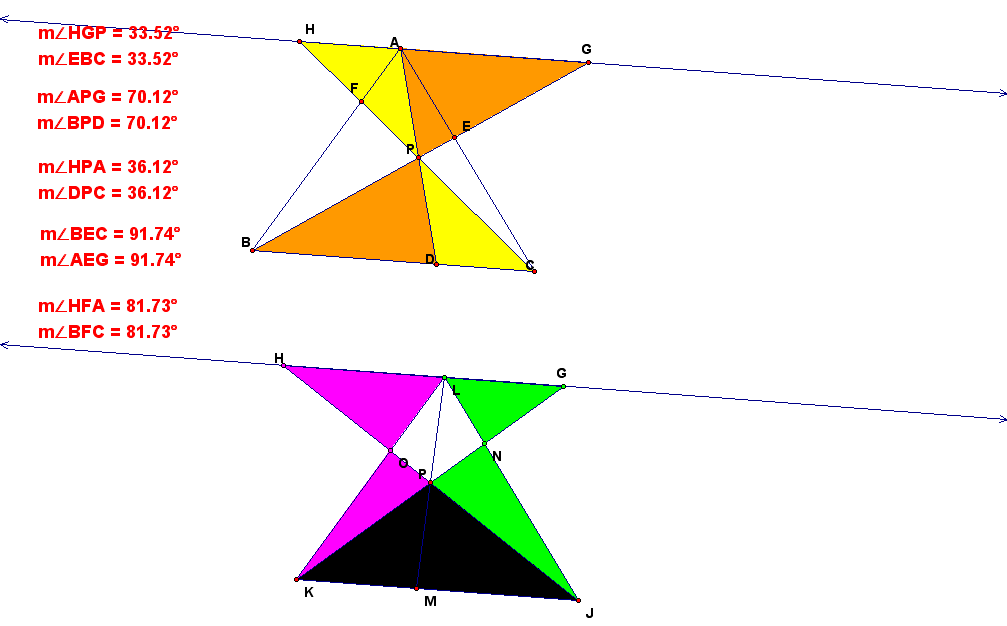

You can see t he proof process by clicking here~

C. The last thing is to show that when P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEFis always greater than or equal to 4. When is it equal to 4?